题目内容
已知函数f（x）满足：f（p+q）=f（p）f（q），f（1）=3，则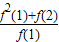
+
+
+
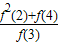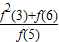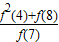等于（ ）A．36
B．24
C．18
D．12
【答案】分析：由题中条件：“f（m+n）=f（m）f（n）”利用赋值法得到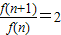
和f（2n）=f2（n），后化简所求式子即得．
解答：解：由f（p+q）=f（p）f（q），
令p=q=n，得f2（n）=f（2n）．
原式=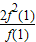
+
+
+
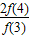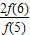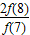
=2f（1）+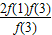
+
+
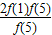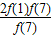
=8f（1）=24．
故选B．
点评：本题主要考查了抽象函数及其应用，考查分析问题和解决问题的能力，属于基础题．
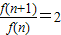和f（2n）=f2（n），后化简所求式子即得．解答：解：由f（p+q）=f（p）f（q），
令p=q=n，得f2（n）=f（2n）．
原式=
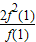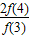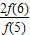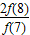
+++=2f（1）+
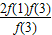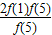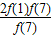
++=8f（1）=24．
故选B．
点评：本题主要考查了抽象函数及其应用，考查分析问题和解决问题的能力，属于基础题．
练习册系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
相关题目