题目内容
在锐角△ABC中，b=2，B=
，sin2A+sin（A-C）-sinB=0，则△ABC的面积为______．
| π |
| 3 |
∵A+B+C=π，∴B=π-（A+C），
∴sinB=sin[π-（A+C）]=sin（A+C），
代入sin2A+sin（A-C）-sinB=0得：sin2A-[sin（A+C）-sin（A-C）]=0，
变形得：2sinAcosA-2cosAsinC=0，即2cosA（sinA-sinC）=0，
所以cosA=0或sinA=sinC，
解得A=
（又锐角△ABC，此情况不满足，舍去）或A=C，
所以A=C，又B=
，b=2，
所以△ABC为边长为2的等边三角形，
则△ABC的面积S=
×22=
．
故答案为：
∴sinB=sin[π-（A+C）]=sin（A+C），
代入sin2A+sin（A-C）-sinB=0得：sin2A-[sin（A+C）-sin（A-C）]=0，
变形得：2sinAcosA-2cosAsinC=0，即2cosA（sinA-sinC）=0，
所以cosA=0或sinA=sinC，
解得A=
| π |
| 2 |
所以A=C，又B=
| π |
| 3 |
所以△ABC为边长为2的等边三角形，
则△ABC的面积S=
| ||
| 4 |
| 3 |
故答案为：
| 3 |
练习册系列答案
相关题目
的取值范围是（ ）
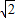，2）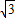
）
）
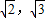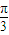，sin2A+sin（A-C）-sinB=0，则△ABC的面积为 ．