题目内容
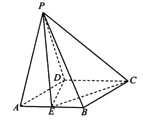
【题目】在四棱锥![]() 中,底面是边长为2的菱形,
中,底面是边长为2的菱形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)证明: ![]() ;
;
(2)求二面角![]() 的正切值.
的正切值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)连接BD,在△ADB中,AD=AB,∠BAD=60°,可得△ADB是等边三角形.可得DE⊥AB.可得CD⊥平面PDE,即可证明PE⊥CD.
(2)作DM⊥PE,垂足为M,连接DM,CM,由CD⊥平面PDE,可得CM⊥PE,∠CMD是二面角C﹣PE﹣D的平面角.由CD⊥平面PDE,可得AB⊥PE.于是PE=3.在△PDE中,作EH⊥PD,H为垂足,可得sin∠EDP=![]()
![]() .在
.在![]() 中,可得
中,可得![]() .
.
试题解析:
(1)在菱形![]() 中,因为
中,因为![]() ,
, ![]() 为
为![]() 的中点,可得
的中点,可得
![]() ,又因为
,又因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
因此![]() .
.
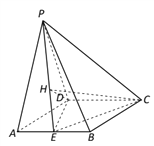
(2)过![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .
.
由![]() 平面
平面![]() ,得
,得![]() ,
,
所以![]() 是二面角
是二面角![]() 的平面角.
的平面角.
由![]() ,
, ![]() ,可得
,可得![]() ,
,
由![]() 为
为![]() 中点,
中点, ![]() ,所以
,所以![]() .
.
又![]() ,
, ![]()
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
故![]() ,
,
所以![]() .
.
在![]() 中,可得
中,可得![]() .
.
所以,二面角![]() 的正切值为
的正切值为![]() .
.

练习册系列答案
相关题目