题目内容
17.已知函数y=$\sqrt{3}$sin4x+cos4x.(1)求它的周期,最大值,最小值;
(2)求它的单调递增区间;
(3)它可以由y=sinx的图象经过怎样的变化得到?
分析 (1)首先,借助于辅助角公式,化简函数解析式人,然后,确定其周期和最值;
(2)直接利用正弦函数的单调区间进行确定即可;
(3)借助于三角函数的图象变换进行表述即可.
解答 解:(1)∵y=$\sqrt{3}$sin4x+cos4x.
=2sin(4x+$\frac{π}{6}$),
∴f(x)=2sin(4x+$\frac{π}{6}$).
∴它的周期T=$\frac{2π}{4}$=$\frac{π}{2}$,最大值2,最小值-2;
(2)∵-$\frac{π}{2}$+2kπ≤4x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,k∈Z,
∴-$\frac{2π}{3}$+2kπ≤4x≤$\frac{π}{3}$+2kπ,
∴-$\frac{π}{6}$+$\frac{1}{2}$kπ≤x≤$\frac{π}{12}$+$\frac{1}{2}$kπ,
∴单调递增区间[-$\frac{π}{6}$+$\frac{1}{2}$kπ,$\frac{π}{12}$+$\frac{1}{2}$kπ],k∈Z;
(3)将函数y=sinx的图象上所以各点向左平移$\frac{π}{6}$个单位,然后,纵坐标不变,横坐标缩短到原来是的$\frac{1}{4}$倍,然后,再将所得函数图象上所有各点的横坐标不变,纵坐标伸长到原来的2倍即可.
点评 本题重点考查了辅助角公式、二倍角公式、三角函数的图象变换等知识,属于中档题.

练习册系列答案
相关题目
5.函数f(x)=xex+a在R上取得最小值1-$\frac{1}{e}$,则函数g(x)=$\frac{f(x)}{{e}^{x}}$在区间(-∞,0)上一定( )
| A. | 有最小值 | B. | 有最大值 | C. | 是减函数 | D. | 是增函数 |
6.下列说法错误的是( )
| A. | 一个算法应包含有限的操作步骤,而不能是无限的 | |
| B. | 有的算法执行完后,可能有无数个结果 | |
| C. | 一个算法可以有0个或多个输入 | |
| D. | 算法中的每一步都是确定的,算法的含义是唯一的 |
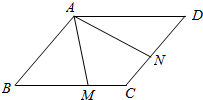 如图,已知菱形ABCD的边长为2,∠BAD=120°,M,N分别为BC、CD上的点,$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,$\overrightarrow{DN}$=μ$\overrightarrow{DC}$,λ,μ∈(0,1),记$\overrightarrow{AM}$=$\overrightarrow{a}$,$\overrightarrow{AN}$=$\overrightarrow{b}$.
如图,已知菱形ABCD的边长为2,∠BAD=120°,M,N分别为BC、CD上的点,$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,$\overrightarrow{DN}$=μ$\overrightarrow{DC}$,λ,μ∈(0,1),记$\overrightarrow{AM}$=$\overrightarrow{a}$,$\overrightarrow{AN}$=$\overrightarrow{b}$.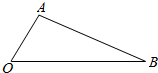 如图所示,在△AOB中,已知∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,则△AOC为钝角三角形的概率为$\frac{2}{5}$.
如图所示,在△AOB中,已知∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,则△AOC为钝角三角形的概率为$\frac{2}{5}$.