题目内容
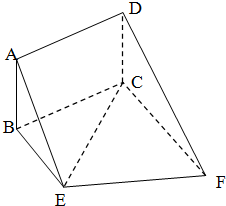 (2012•眉山二模)如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=
(2012•眉山二模)如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=| π |
| 2 |
| 3 |
(1)证明:AE∥平面DCF;
(2)当AB的长为何值时,二面角A-EF-C为
| π |
| 3 |
(3)在(2)的条件下,求几何体ABE-DCF的体积.
分析:(1)过点E作EG⊥CF交CF于G,连接DG,证明四边形ADGE为平行四边形,可得AE∥DG,结合线面平行的判定定理,即可得到AE∥平面DCF;
(2)过点B作BH⊥FE交FE的延长线于H,连接AH,证明∠AHB是二面角A-EF-C的平面角,求得BH=BCsin∠BEH=
,即可求得AB的长;
(3)连接AF,FB,则几何体ABE-DCF的体积为V=VF-ABE+VF-ABCD,由此可得结论.
(2)过点B作BH⊥FE交FE的延长线于H,连接AH,证明∠AHB是二面角A-EF-C的平面角,求得BH=BCsin∠BEH=
3
| ||
| 2 |
(3)连接AF,FB,则几何体ABE-DCF的体积为V=VF-ABE+VF-ABCD,由此可得结论.
解答:(1)证明:过点E作EG⊥CF交CF于G,连接DG,
可得四边形BCGE为矩形,又ABCD为矩形
所以AD∥EG且AD=EG,从而四边形ADGE为平行四边形
故AE∥DG
因为AE?平面DCF,DG?平面DCF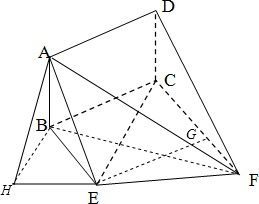
所以AE∥平面DCF
(2)解:∵平面ABCD⊥平面BEFC,AB⊥BC,∴AB⊥平面BEFC
过点B作BH⊥FE交FE的延长线于H,连接AH,∴AH⊥FE.
故∠AHB是二面角A-EF-C的平面角.
在Rt△EFG中,因为EG=AD=
,EF=2,所以∠CFE=60°,GF=1.
∵∠CEF=
,∴CF=4,∴BE=GC=3
∴BH=BCsin∠BEH=
∴AB=BHtan∠AHB=
×
=
∴当AB的长为
时,二面角A-EF-C为
.
(3)解:连接AF,FB,则几何体ABE-DCF的体积为V=VF-ABE+VF-ABCD=
×
×
×3×
+
×
×
×4=
.
可得四边形BCGE为矩形,又ABCD为矩形
所以AD∥EG且AD=EG,从而四边形ADGE为平行四边形
故AE∥DG
因为AE?平面DCF,DG?平面DCF

所以AE∥平面DCF
(2)解:∵平面ABCD⊥平面BEFC,AB⊥BC,∴AB⊥平面BEFC
过点B作BH⊥FE交FE的延长线于H,连接AH,∴AH⊥FE.
故∠AHB是二面角A-EF-C的平面角.
在Rt△EFG中,因为EG=AD=
| 3 |
∵∠CEF=
| π |
| 2 |
∴BH=BCsin∠BEH=
3
| ||
| 2 |
∴AB=BHtan∠AHB=
3
| ||
| 2 |
| 3 |
| 9 |
| 2 |
∴当AB的长为
| 9 |
| 2 |
| π |
| 3 |
(3)解:连接AF,FB,则几何体ABE-DCF的体积为V=VF-ABE+VF-ABCD=
| 1 |
| 3 |
| 1 |
| 2 |
| 9 |
| 2 |
| 3 |
| 1 |
| 3 |
| 9 |
| 2 |
| 3 |
33
| ||
| 4 |
点评:本题考查空间直线、平面位置关系的判断,二面角大小求解,考查几何体体积的计算,属于中档题.

练习册系列答案
相关题目
 (2012•眉山二模)某市高三调研考试中,对数学在90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若130~140分数段的人数为90,那么90~100分数段的人数为( )
(2012•眉山二模)某市高三调研考试中,对数学在90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若130~140分数段的人数为90,那么90~100分数段的人数为( )