题目内容
设数列{ }满足:a1=2,对一切正整数n,都有
}满足:a1=2,对一切正整数n,都有
(1)探讨数列{ }是否为等比数列,并说明理由;
}是否为等比数列,并说明理由;
(2)设
(1)是,理由见解析;(2)证明过程详见解析.
解析试题分析:本题主要考查等比数列的定义、等比数列的证明、数学归纳法、放缩法等数学知识,考查学生的分析问题解决问题的能力、转化能力和计算能力.第一问,通过对已知表达式的移项,变形可得出数列的通项 ,可以用等比数列的定义证明也可以用数学归纳法证明;第二问,将第一问的结论代入,得到
,可以用等比数列的定义证明也可以用数学归纳法证明;第二问,将第一问的结论代入,得到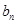 表达式,法一:利用放缩法和裂项相消法证明,法二:利用数列的累加法和放缩法证明.
表达式,法一:利用放缩法和裂项相消法证明,法二:利用数列的累加法和放缩法证明.
试题解析:⑴由 得
得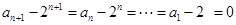 ,
,
∴对一切 ,可知
,可知 是首项为
是首项为 ,公比为
,公比为 的等比数列. 5分
的等比数列. 5分
(通过归纳猜想,使用数学归纳法证明的,亦应给分)
(2)由(1)知 6分
6分
证一:
 10分
10分 12分
12分
证二:∵ ≥
≥ (仅当
(仅当 时等号成立),故此,
时等号成立),故此, ≤
≤ 10分
10分
从而,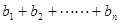 ≤
≤
 <
< 12分
12分
考点:1.数学归纳法;2.累加法;3.放缩法.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 ≤
≤ .
. 中,已知
中,已知 ,
, ,
, (
( ,
, ).
). ,
,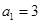 时,分别求
时,分别求 的值,判断
的值,判断 是否为定值,并给出证明;
是否为定值,并给出证明; ,使得
,使得 为完全平方数.
为完全平方数. 计算
计算 由此推测出
由此推测出 的计算公式,并用数学归纳法证明.
的计算公式,并用数学归纳法证明. ;
; ;
; ;
; .
. (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论. ,n∈N+,求a2,a3,a4
,n∈N+,求a2,a3,a4
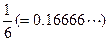 是无限小数,所以
是无限小数,所以 是无理数。”
是无理数。”