题目内容
“无理数是无限小数,而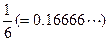 是无限小数,所以
是无限小数,所以 是无理数。”
是无理数。”
这个推理是 _推理(在“归纳”、“类比”、“演绎”中选择填空)
演绎
解析

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
题目内容
“无理数是无限小数,而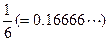 是无限小数,所以
是无限小数,所以 是无理数。”
是无理数。”
这个推理是 _推理(在“归纳”、“类比”、“演绎”中选择填空)
演绎
解析

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案