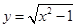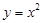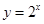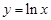题目内容
设函数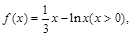 则
则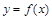 ( )
( )
A.在区间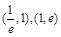 内均有零点 内均有零点 |
B.在区间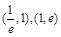 内均无零点 内均无零点 |
C.在区间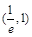 内无零点,在区间 内无零点,在区间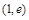 内有零点 内有零点 |
D.在区间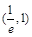 内有零点,在区间 内有零点,在区间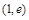 内无零点 内无零点 |
C
解析试题分析:分别代入可得 ,
, ,
, ,所以根据函数的零点存在定理可知函数
,所以根据函数的零点存在定理可知函数 在区间
在区间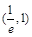 内无零点,在区间
内无零点,在区间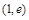 内有零点.
内有零点.
考点:本小题主要考查函数的零点存在定理的应用.
点评:函数的零点存在定理可以判断在某个区间是有没有零点,但是不能确定零点的个数.

练习册系列答案
相关题目
函数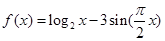 零点的个数是 ( )
零点的个数是 ( )
| A.5 | B.4 | C.3 | D.2 |
使得函数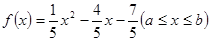 的值域为
的值域为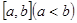 的实数对
的实数对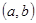
有( )对
| A.1 | B.2 | C.3 | D.无数 |
函数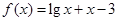 的零点所在区间为
的零点所在区间为
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,+∞) |
函数 的值域是( )
的值域是( )
A. | B. | C. | D. |
已知定义在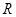 上的偶函数
上的偶函数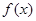 满足
满足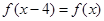 ,且在区间[0,2]上
,且在区间[0,2]上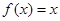 ,若关于
,若关于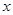 的方程
的方程 有三个不同的根,则
有三个不同的根,则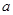 的范围为
的范围为
A.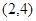 | B.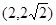 | C.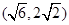 | D.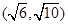 |
已知函数 的定义域为
的定义域为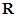 ,满足
,满足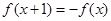 ,且当
,且当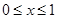 时,
时,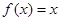 ,
,
则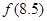 等于( )
等于( )
A.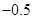 | B.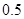 | C.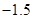 | D.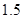 |
函数y=x+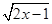 ( )
( )
A.有最小值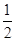 ,无最大值 ,无最大值 |
B.有最大值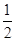 ,无最小值 ,无最小值 |
C.有最小值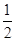 ,最大值2 ,最大值2 |
| D.无最大值,也无最小值 |
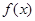 ,如果存在锐角
,如果存在锐角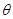 使得
使得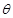 ,所得曲线仍是一函数,则称函数
,所得曲线仍是一函数,则称函数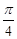 的旋转性的是( )
的旋转性的是( )