题目内容
函数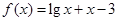 的零点所在区间为
的零点所在区间为
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,+∞) |
C
解析试题分析:解:∵函数f(x)=x+lgx-3,(x>0)∴f′(x)=1+ ,∴f′(x)>0,∴f(x)为增函数, f(2)=2+lg2-3=lg2-1<0,f(3)=3+lg3-3=lg3>0,f(2)f(3)<0当x>3时,f(x)>0,当x<2时,f(x)<0,∴函数f(x)=x+lgx-3的零点所在区间为(2,3);故选C;
,∴f′(x)>0,∴f(x)为增函数, f(2)=2+lg2-3=lg2-1<0,f(3)=3+lg3-3=lg3>0,f(2)f(3)<0当x>3时,f(x)>0,当x<2时,f(x)<0,∴函数f(x)=x+lgx-3的零点所在区间为(2,3);故选C;
考点:函数的零点
点评:此题主要考查函数的零点问题,是一道基础题,考查零点定理的应用,考查的知识点比较全面。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
下列整数中,小于-3的整数是
| A.-4 | B.-2 | C.0 | D.3 |
已知关于x的函数y=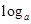 (2-ax)在[0,1]上是减函数,则a的取值范围是
(2-ax)在[0,1]上是减函数,则a的取值范围是
| A.(0,1) | B.(1,2) | C.(0,2) | D.[2,+∞)] |
函数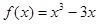 的递减区间是
的递减区间是
A. 或 或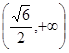 | B.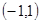 |
C.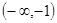 或 或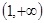 | D.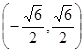 |
设函数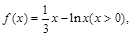 则
则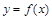 ( )
( )
A.在区间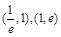 内均有零点 内均有零点 |
B.在区间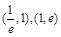 内均无零点 内均无零点 |
C.在区间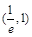 内无零点,在区间 内无零点,在区间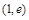 内有零点 内有零点 |
D.在区间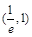 内有零点,在区间 内有零点,在区间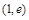 内无零点 内无零点 |
函数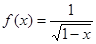 的定义域是( )
的定义域是( )
A.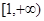 | B.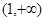 | C.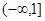 | D.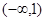 |
下列各函数中为奇函数的是( )
A.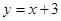 | B.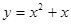 | C.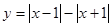 | D.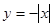 |
定义在R上的奇函数 在(0,+∞)上是增函数,又
在(0,+∞)上是增函数,又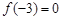 ,则不等式
,则不等式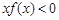 的解集为( )
的解集为( )
| A.(-3,0)∪(0,3) | B.(-∞,-3)∪(3,+∞) |
| C.(-3,0)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
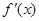 是
是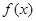 的导函数,
的导函数,