题目内容
8.已知△ABC为等腰直角三角形,|CA|=|CB|,|AB|=4,O为AB中点,动点P满足条件:|PO|2=|PA|•|PB|,则线段CP长的最小值为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 4 |
分析 以AB所在直线为x轴,O为坐标原点,建立平面直角坐标系,求出P的轨迹方程,即可得出结论.
解答 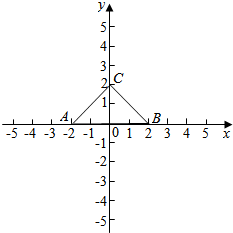 解:以AB所在直线为x轴,O为坐标原点,建立平面直角坐标系.则A(-2,0),B(2,0)、C(0,2).
解:以AB所在直线为x轴,O为坐标原点,建立平面直角坐标系.则A(-2,0),B(2,0)、C(0,2).
设P(x,y),则
∵|PO|2=|PA|•|PB|,
∴x2+y2=$\sqrt{(x+2)^{2}+{y}^{2}}$•$\sqrt{(x-2)^{2}+{y}^{2}}$
∴x2-y2-2=0.
∴CP=$\sqrt{{x}^{2}+(y-2)^{2}}$=$\sqrt{2(y-1)^{2}+4}$
∴y=1时,CP有最小值2.
故选:B.
点评 本题考查轨迹方程,考查学生的计算能力,确定轨迹方程是关键.

练习册系列答案
相关题目
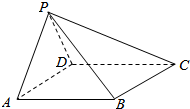 如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°.
如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°.