题目内容
13.函数y=|5sin(2x+$\frac{π}{3}$)|的最小正周期为$\frac{π}{2}$.分析 首先求出y=5sin(2x+$\frac{π}{3}$)的周期,进一步利用y=|5sin(2x+$\frac{π}{3}$)|的周期为y=5sin(2x+$\frac{π}{3}$)的周期的一半,
求出结论.
解答 解:y=5sin(2x+$\frac{π}{3}$)的周期为:$T=\frac{2π}{2}=π$,
由于y=|5sin(2x+$\frac{π}{3}$)|的周期为y=5sin(2x+$\frac{π}{3}$)的周期的一半,
所以:y=|5sin(2x+$\frac{π}{3}$)|的周期为$\frac{π}{2}$,
故答案为:$\frac{π}{2}$.
点评 本题考查的知识要点:正弦型函数周期的求法,主要考察正弦型函数的性质.

练习册系列答案
相关题目
2.已知复数z=$\frac{1+2i}{2-i}$(i为虚数单位),则z的虚部为( )
| A. | -1 | B. | 0 | C. | 1 | D. | i |

 如图是某中学参加高三体育考试的学生中抽取60名学生的体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图中的信息回答下列问题:
如图是某中学参加高三体育考试的学生中抽取60名学生的体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图中的信息回答下列问题: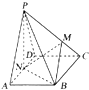 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点. 如图,在五面体ABCDEF中,四边形 ABCD是边长为4的正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.
如图,在五面体ABCDEF中,四边形 ABCD是边长为4的正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.