题目内容
如图,函数y=2sin(πx+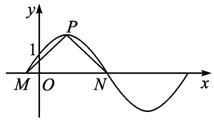
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)设P是图象上的最高点,M、N是图象与x轴的交点,求PM与PN的夹角.
解:(Ⅰ)把x=0,y=1代入y=2sin(πx+![]() ),得2sin
),得2sin![]() =1.
=1.
∴sin![]() =
=![]() .又0≤
.又0≤![]() ≤
≤![]() ,
,
∴![]() =
=![]() .
.
(Ⅱ)过PE⊥MN,垂足为E,设∠MPE=θ,则PE=2,ME=![]() T=
T=![]() ·
·![]() =
=![]() .
.
∴tanθ=![]() =
=![]() =
=![]() .tan∠MPN=tan2θ=
.tan∠MPN=tan2θ= .
.
因此PM与PN的夹角为arctan![]() .
.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤
如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤ 已知如图是函数y=2sin(ωx+φ)(|φ|<
已知如图是函数y=2sin(ωx+φ)(|φ|< 如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤
如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤ 如图,函数y=2sin(πx+φ),x∈R(其中0<φ≤
如图,函数y=2sin(πx+φ),x∈R(其中0<φ≤ 如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤
如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤