题目内容
已知 ,将f (x)的图象向左平移
,将f (x)的图象向左平移 ,再向上平移2个长度单位后,图象关于直线
,再向上平移2个长度单位后,图象关于直线 对称.
对称.
(1)求实数a的值,并求f(x)取得最大值时x的集合;
(2)求f(x)的单调递增区间.
解:(1)∵已知 =-2-2cos2x+2
=-2-2cos2x+2 a•sin2x,
a•sin2x,
将f(x)的图象向左平移 所得图象对应的函数为y=-2-2cos2(x+
所得图象对应的函数为y=-2-2cos2(x+ )+2
)+2 a•sin2(x+
a•sin2(x+ )=-2+2sin2x+2
)=-2+2sin2x+2 a•cos2x,
a•cos2x,
再把所得图象向上平移2个长度单位后,所得图象对应的函数为y=2sin2x+2 a•cos2x,
a•cos2x,
∴g(x)=2sin2x+2 a•cos2x.
a•cos2x.
∵g(x)的图象关于直线x= 对称,∴有g(0)=g(
对称,∴有g(0)=g( ),即2
),即2 a=
a= +
+ a,解得a=1.
a,解得a=1.
则f(x)=2 sin2x-2cos2x-2=4sin(2x-
sin2x-2cos2x-2=4sin(2x- )-2.
)-2.
当2x- =2kπ+
=2kπ+ ,即x=kπ+
,即x=kπ+ 时,f(x)取得最大值2.
时,f(x)取得最大值2.
因此,f(x)取得最大值时x的集合是{x|x=kπ+ ,k∈Z}.
,k∈Z}.
(2)令2kπ- ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,求得 kπ-
,k∈z,求得 kπ- ≤x≤kπ+
≤x≤kπ+ ,
,
因此,f(x)的单调递增区间是[kπ- ,kπ+
,kπ+ ](k∈Z).
](k∈Z).
分析:(1)先求得将f(x)的图象变换后所得图象对应的函数解析式为 g(x)=2sin2x+2 a•cos2x,由g(x)的图象关于直线x=
a•cos2x,由g(x)的图象关于直线x= 对称,g(0)=g(
对称,g(0)=g( ),求得a的值,从而求得f(x)的解析式,由此可得f(x)的最大值.
),求得a的值,从而求得f(x)的解析式,由此可得f(x)的最大值.
(2)令2kπ- ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,求得x的范围,即可求得f(x)的单调递增区间.
,k∈z,求得x的范围,即可求得f(x)的单调递增区间.
点评:本题考查三角函数的最值,重点考查正弦函数的对称性质与单调性,难点是辅助角公式的理解与应用,属于中档题.
 =-2-2cos2x+2
=-2-2cos2x+2 a•sin2x,
a•sin2x,将f(x)的图象向左平移
 所得图象对应的函数为y=-2-2cos2(x+
所得图象对应的函数为y=-2-2cos2(x+ )+2
)+2 a•sin2(x+
a•sin2(x+ )=-2+2sin2x+2
)=-2+2sin2x+2 a•cos2x,
a•cos2x,再把所得图象向上平移2个长度单位后,所得图象对应的函数为y=2sin2x+2
 a•cos2x,
a•cos2x,∴g(x)=2sin2x+2
 a•cos2x.
a•cos2x.∵g(x)的图象关于直线x=
 对称,∴有g(0)=g(
对称,∴有g(0)=g( ),即2
),即2 a=
a= +
+ a,解得a=1.
a,解得a=1. 则f(x)=2
 sin2x-2cos2x-2=4sin(2x-
sin2x-2cos2x-2=4sin(2x- )-2.
)-2. 当2x-
 =2kπ+
=2kπ+ ,即x=kπ+
,即x=kπ+ 时,f(x)取得最大值2.
时,f(x)取得最大值2.因此,f(x)取得最大值时x的集合是{x|x=kπ+
 ,k∈Z}.
,k∈Z}.(2)令2kπ-
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,求得 kπ-
,k∈z,求得 kπ- ≤x≤kπ+
≤x≤kπ+ ,
,因此,f(x)的单调递增区间是[kπ-
 ,kπ+
,kπ+ ](k∈Z).
](k∈Z).分析:(1)先求得将f(x)的图象变换后所得图象对应的函数解析式为 g(x)=2sin2x+2
 a•cos2x,由g(x)的图象关于直线x=
a•cos2x,由g(x)的图象关于直线x= 对称,g(0)=g(
对称,g(0)=g( ),求得a的值,从而求得f(x)的解析式,由此可得f(x)的最大值.
),求得a的值,从而求得f(x)的解析式,由此可得f(x)的最大值.(2)令2kπ-
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,求得x的范围,即可求得f(x)的单调递增区间.
,k∈z,求得x的范围,即可求得f(x)的单调递增区间.点评:本题考查三角函数的最值,重点考查正弦函数的对称性质与单调性,难点是辅助角公式的理解与应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
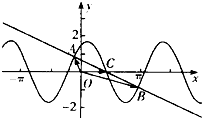 已知函数y=f(x)的图象可由y=sinx的图象经过如下变换得到:
已知函数y=f(x)的图象可由y=sinx的图象经过如下变换得到: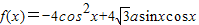 ,将f (x)的图象向左平移
,将f (x)的图象向左平移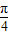 ,再向上平移2个长度单位后,图象关于直线
,再向上平移2个长度单位后,图象关于直线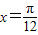 对称.
对称.