题目内容
已知直线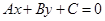
与圆
相交于
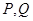两点，其中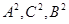
成等差数列，
为坐标原点，则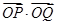
=___________.
．
解析试题分析：设
，当
时，联立
，因为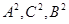成等差数列，所以
，化为
，∴
，
，∵
，∴
，当
时，，可求得
，故答案为．
考点：平面向量数量积的运算；直线与圆的位置关系．
练习册系列答案
相关题目
题目内容
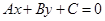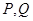已知直线与圆相交于两点，其中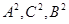成等差数列，为坐标原点，则=___________.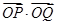
．
解析试题分析：设，当时，联立，因为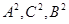成等差数列，所以，化为，∴，，∵，∴，当时，，可求得，故答案为．
考点：平面向量数量积的运算；直线与圆的位置关系．
的边长为
，点
是
边上的动点，则
的值为________，
的最大值为 ．
是边长为
的正方形，若
，
，则
的值为 .
，平面内一点
满足
＝
＋
，则
＝ .
中，
，
，
，
，
，
为线段
（含端点）上一个动点，设
，
，对于函数
，给出以下三个结论：①当
时，函数
的值域为
；
，都有
成立；
.
满足
，则
面积的最大值为 
中，
，
，
，则
.
为弧上的动点，
与
交于点
，则
最小值是________________.
·
= .