题目内容
如图,在直角梯形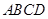 中,
中,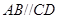 ,
,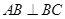 ,
,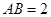 ,
,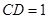 ,
,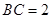 ,
,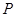 为线段
为线段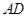 (含端点)上一个动点,设
(含端点)上一个动点,设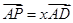 ,
, ,对于函数
,对于函数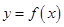 ,给出以下三个结论:①当
,给出以下三个结论:①当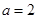 时,函数
时,函数 的值域为
的值域为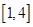 ;
;
②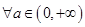 ,都有
,都有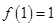 成立;
成立;
③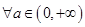 ,函数
,函数 的最大值都等于
的最大值都等于 .
.
其中所有正确结论的序号是_________.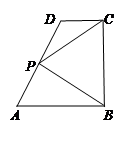

②③.
解析试题分析:以点 为坐标原点,
为坐标原点, 、
、 所在直线分别为
所在直线分别为 轴、
轴、 轴建立如图所示的平面直角坐标系
轴建立如图所示的平面直角坐标系 ,则
,则 、
、 、
、 、
、 ,设点
,设点 ,
, ,
, ,
,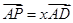 ,则有
,则有 ,解得
,解得 ,因此点
,因此点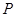 的坐标为
的坐标为 ,
,
因此 ,
, ,
,
所以 ,其中
,其中 ,
,
对于命题①,当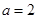 时,
时, ,图象开口向上,对称轴
,图象开口向上,对称轴 ,
,
当 时,
时, 取最小值,即
取最小值,即 ,
,
且 ,
, ,因此
,因此 ,所以函数
,所以函数 的值域为
的值域为 ;
;
对于命题②,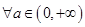 ,
, 成立;
成立;
对于命题③,二次函数 的图象开口向上,对称轴为直线
的图象开口向上,对称轴为直线 ,
,
当 时,即
时,即 时,
时, ,此时,直线
,此时,直线 与对称轴的距离较直线
与对称轴的距离较直线 与对称轴的距离远,此时函数
与对称轴的距离远,此时函数 在
在 处取得最大值,即
处取得最大值,即 ,
,
当 时,即当
时,即当 时,函数
时,函数 在区间
在区间 上单调递减,
上单调递减,
此时函数 在
在 处取得最大值,即
处取得最大值,即 ,
,
综上所述,正确结论的序号是②③.
考点:1.平面向量的数量积;2.二次函数

练习册系列答案
相关题目
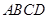 的边长为
的边长为 ,记以
,记以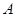 为起点,其余顶点为终点的向量分别为
为起点,其余顶点为终点的向量分别为 ,
, ,
, .若
.若 且
且 ,则
,则 的所有可能取值为 .
的所有可能取值为 . 的夹角为 .
的夹角为 .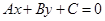 与圆
与圆 相交于
相交于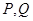 两点,其中
两点,其中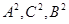 成等差数列,
成等差数列, 为坐标原点,则
为坐标原点,则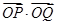 =___________.
=___________. 的斜边BC上的两个三等分点,已知AB=3,AC=6,则·= .
的斜边BC上的两个三等分点,已知AB=3,AC=6,则·= .
 的取值范围为________.
的取值范围为________. 中,若
中,若 ,
, ,则
,则 ________
________ 的范围是__________.
的范围是__________.