Question

12．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+2x}&{x＞0}\\{1}&{x=0}\\{-x-1}&{x＜0}\end{array}\right.$
（1）求f（-1），f[f（-1）]，f{f[f（-1）]}的值；
（2）画出函数的图象．

Answer 1

分析 （1）根据分段函数，分别求出对应的函数值即可，
（2）根据分段函数，画出相对应的图象即可．

解答 解：（1）∵f（x）=$\left\{\begin{array}{l}{-{x}^{2}+2x}&{x＞0}\\{1}&{x=0}\\{-x-1}&{x＜0}\end{array}\right.$
∴f（-1）=-（-1）-1=0，f[f（-1）]=f（0）=1，f{f[f（-1）]}=f（1）=-1+2=1，
（2）图象如图所示：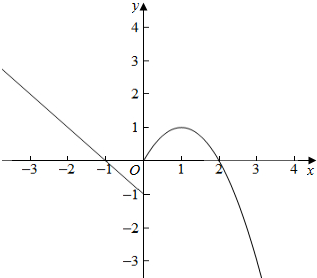

点评 本题主要考查了函数值得求法和函数图象的画法，属于基础题．