题目内容
(本题满分12分)已知函数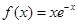 ,
,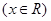 .
.
(1)求函数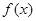 的单调区间和极值;
的单调区间和极值;
(2)已知函数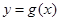 的图象与函数
的图象与函数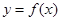 的图象关于直线
的图象关于直线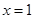 对称;
对称;
证明:当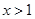 时,
时,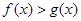
(3)如果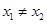 且
且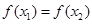 ,证明
,证明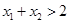
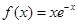 ,
,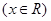 .
.(1)求函数
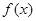 的单调区间和极值;
的单调区间和极值;(2)已知函数
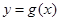 的图象与函数
的图象与函数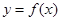 的图象关于直线
的图象关于直线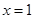 对称;
对称;证明:当
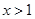 时,
时,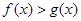
(3)如果
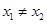 且
且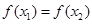 ,证明
,证明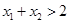
(Ⅰ)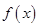 在区间
在区间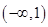 内是增函数,在区间
内是增函数,在区间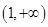 内是减函数.
内是减函数.
函数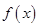 在
在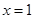 处取得极大值
处取得极大值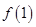 .且
.且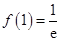 .
.
(Ⅱ)见解析;(Ⅲ)见解析。
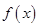 在区间
在区间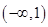 内是增函数,在区间
内是增函数,在区间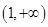 内是减函数.
内是减函数.函数
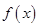 在
在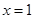 处取得极大值
处取得极大值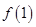 .且
.且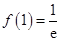 .
.(Ⅱ)见解析;(Ⅲ)见解析。
本试题主要是考查了运用导数研究函数的性质的综合运用。
(1)利用导数,结合导数的符号与函数单调性的关系得到第一问中的单调区间和极值问题。
(2)先利用对称性求解函数的解析式,然后构造函数证明不等式恒成立,或者利用第一问的结论,结合对称性得到证明。
(3)由上可知函数的的单调性,结合性质可知不等式的证明。
(Ⅰ)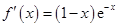 .令
.令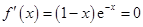 ,则
,则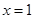 .
.
当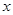 变化时,
变化时,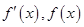 的变化情况如下表:
的变化情况如下表:
所以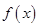 在区间
在区间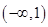 内是增函数,在区间
内是增函数,在区间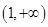 内是减函数.
内是减函数.
函数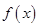 在
在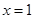 处取得极大值
处取得极大值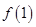 .且
.且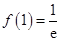 .
.
(Ⅱ)因为函数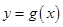 的图象与函数
的图象与函数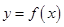 的图象关于直线
的图象关于直线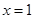 对称,
对称,
所以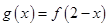 ,于是
,于是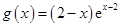 .
.
记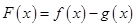 ,则
,则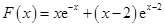 ,
,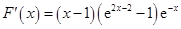 ,
,
当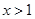 时,
时,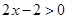 ,从而
,从而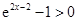 ,又
,又 ,所以
,所以 ,
,
于是函数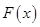 在区间
在区间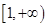 上是增函数.
上是增函数.
因为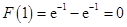 ,所以,当
,所以,当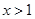 时,
时,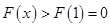 .因此
.因此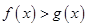 .
.
(Ⅲ)(1) 若 ,由(Ⅰ)及
,由(Ⅰ)及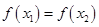 ,得
,得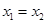 ,与
,与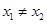 矛盾;
矛盾;
(2) 若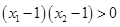 ,由(Ⅰ)及
,由(Ⅰ)及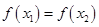 ,得
,得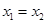 ,与
,与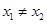 矛盾;
矛盾;
根据(1),(2)可得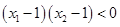 .不妨设
.不妨设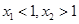 .
.
由(Ⅱ)可知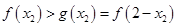 ,所以
,所以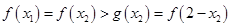 .
.
因为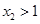 ,所以
,所以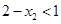 ,又
,又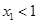 ,由(Ⅰ),
,由(Ⅰ),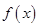 在区间
在区间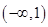 内是增函数,
内是增函数,
所以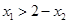 ,即
,即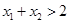 .
.
(1)利用导数,结合导数的符号与函数单调性的关系得到第一问中的单调区间和极值问题。
(2)先利用对称性求解函数的解析式,然后构造函数证明不等式恒成立,或者利用第一问的结论,结合对称性得到证明。
(3)由上可知函数的的单调性,结合性质可知不等式的证明。
(Ⅰ)
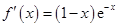 .令
.令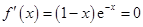 ,则
,则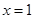 .
.当
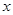 变化时,
变化时,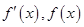 的变化情况如下表:
的变化情况如下表: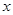 | 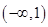 | 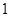 | 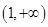 |
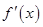 | 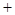 |  | 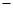 |
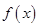 | 增 | 极大值 | 减 |
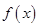 在区间
在区间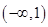 内是增函数,在区间
内是增函数,在区间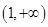 内是减函数.
内是减函数.函数
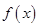 在
在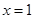 处取得极大值
处取得极大值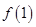 .且
.且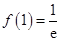 .
.(Ⅱ)因为函数
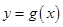 的图象与函数
的图象与函数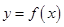 的图象关于直线
的图象关于直线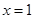 对称,
对称,所以
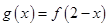 ,于是
,于是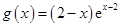 .
.记
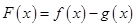 ,则
,则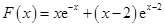 ,
,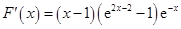 ,
,当
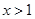 时,
时,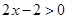 ,从而
,从而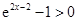 ,又
,又 ,所以
,所以 ,
,于是函数
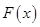 在区间
在区间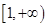 上是增函数.
上是增函数.因为
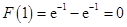 ,所以,当
,所以,当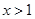 时,
时,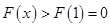 .因此
.因此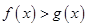 .
.(Ⅲ)(1) 若
 ,由(Ⅰ)及
,由(Ⅰ)及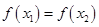 ,得
,得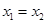 ,与
,与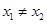 矛盾;
矛盾;(2) 若
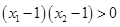 ,由(Ⅰ)及
,由(Ⅰ)及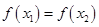 ,得
,得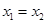 ,与
,与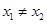 矛盾;
矛盾;根据(1),(2)可得
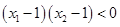 .不妨设
.不妨设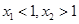 .
.由(Ⅱ)可知
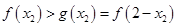 ,所以
,所以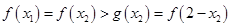 .
.因为
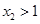 ,所以
,所以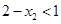 ,又
,又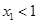 ,由(Ⅰ),
,由(Ⅰ),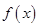 在区间
在区间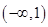 内是增函数,
内是增函数,所以
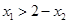 ,即
,即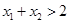 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
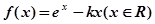
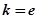 ,试确定函数
,试确定函数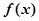 的单调区间;
的单调区间;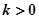 且对任意
且对任意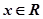 ,
,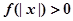 恒成立,试确定实数
恒成立,试确定实数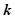 的取值范围;
的取值范围;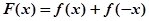 ,求证:
,求证: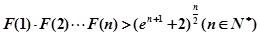
 在区间
在区间 上的最值.
上的最值.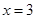 是函数
是函数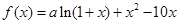 的一个极值点。
的一个极值点。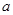 ;
;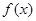 的单调区间;
的单调区间;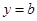 与函数
与函数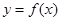 的图象有3个交点,求
的图象有3个交点,求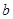 的取值范围。
的取值范围。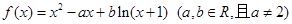
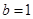 且函数
且函数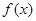 在其定义域上为增函数时,求
在其定义域上为增函数时,求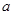 的取值范围;
的取值范围;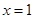 处取得极值,试用
处取得极值,试用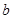 ;
;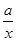 .
. 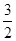 ,求a的值;
,求a的值;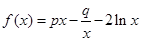 ,且
,且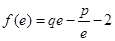 ,其中
,其中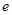 是自然对数的底数.
是自然对数的底数.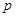 与
与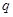 的关系;
的关系;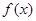 在其定义域内为单调函数,求
在其定义域内为单调函数,求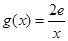 ,若在
,若在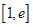 上至少存在一点
上至少存在一点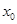 ,使得
,使得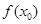 >
> 成立,求实数
成立,求实数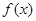 是定义在R上的奇函数,且
是定义在R上的奇函数,且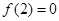 ,当x>0时,有
,当x>0时,有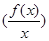 的导数小于零恒成立,则不等式
的导数小于零恒成立,则不等式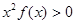 的解集是( )
的解集是( ) (2,+
(2,+ 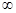 )
) 其中
其中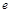 是自然对数的底 .
是自然对数的底 .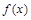 在
在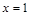 处取得极值,求
处取得极值,求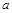 的值;
的值;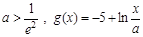 ,存在
,存在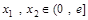 ,使得
,使得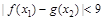 成立,求
成立,求