题目内容
已知向量m=(1, ),n=(2,2
),n=(2,2 )(其中ω为正常数),
)(其中ω为正常数),
(Ⅰ)若ω=1,x∈ ,求m∥n时tanx的值;
,求m∥n时tanx的值;
(Ⅱ)设f(x)=m·n-2,若函数f(x)的图象的相邻两个对称中心的距离为 ,求f(x)在区间[0,
,求f(x)在区间[0, ]上的最小值.
]上的最小值.
 ),n=(2,2
),n=(2,2 )(其中ω为正常数),
)(其中ω为正常数), (Ⅰ)若ω=1,x∈
 ,求m∥n时tanx的值;
,求m∥n时tanx的值;(Ⅱ)设f(x)=m·n-2,若函数f(x)的图象的相邻两个对称中心的距离为
 ,求f(x)在区间[0,
,求f(x)在区间[0, ]上的最小值.
]上的最小值.解:(Ⅰ)m∥n时,
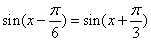 ,
,
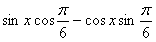
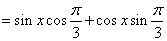 ,
,
则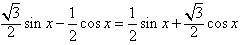 ,
,
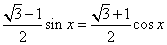 ,
,
所以,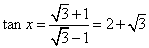 。
。
(Ⅱ)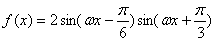
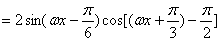
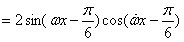
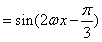 ,
,
∵函数f(x)的图象的相邻两个对称中心的距离为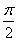 ,
,
∴f(x)的最小正周期为π,
又ω为正常数,
∴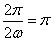 ,解得ω=1,
,解得ω=1,
故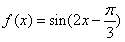 ,
,
因为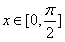 ,所以
,所以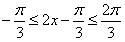 ,
,
故当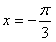 时,f(x)取最小值
时,f(x)取最小值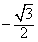 。
。
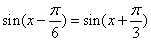 ,
,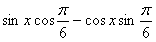
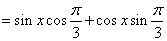 ,
,则
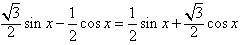 ,
,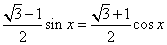 ,
,所以,
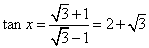 。
。(Ⅱ)
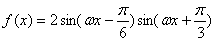
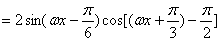
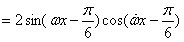
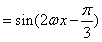 ,
,∵函数f(x)的图象的相邻两个对称中心的距离为
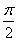 ,
,∴f(x)的最小正周期为π,
又ω为正常数,
∴
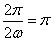 ,解得ω=1,
,解得ω=1,故
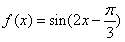 ,
,因为
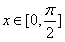 ,所以
,所以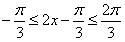 ,
,故当
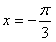 时,f(x)取最小值
时,f(x)取最小值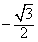 。
。 
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目