题目内容
在各项均为正数的等比数列
中,公比
．若
, 
,
数列
的前
项和为
,则当
取最大值时,的值为（ ）
中,公比．若, ,数列的前项和为,则当取最大值时,的值为（ ）| A．8 | B．9 | C．8或9 | D．17 |
C
试题分析：依题意有
，解得
或
，所以
或
，而
，所以
即
，所以
，所以
，所以数列
是以4为首项，
为公差的等差数列，所以
，所以
，所以数列
是以
为首项，
为公差的等差数列，要使
取得最大值，则必须是数列中所有正数项的和，才会取得最大值，所以由
，而
，所以当
或
时，取得最大值，故选C.项和.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
满足
，
，
，
是数列
的前
项和．
；
满足
，数列
满足
，试比较数列
前
与
的大小；
，
恒成立，求实数
的取值范围．
的值为 ( )．
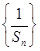的前n项和，问是否存在常数m，使Tn＝m
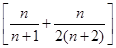，若存在，求m的值；若不存在，说明理由．
满足：
，
，若
，
，且数列
的单调递增数列，则实数
的取值范围为（ ）
的前n项和为
，且
，则
（ ）
,Sn为数列{an}的前n项和，则S8= ；S4n= 。
的前n项和为Sn，且S3=6，a1=4，则公差d等于 ( )