题目内容
如图,已知两条抛物线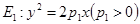 和
和 ,过原点
,过原点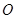 的两条直线
的两条直线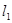 和
和 ,
,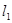 与
与 分别交于
分别交于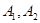 两点,
两点, 与
与 分别交于
分别交于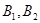 两点.
两点.
(1)证明:
(2)过原点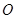 作直线
作直线 (异于
(异于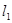 ,
, )与
)与 分别交于
分别交于 两点.记
两点.记 与
与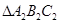 的面积分别为
的面积分别为 与
与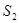 ,求
,求 的值.
的值.

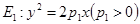 和
和 ,过原点
,过原点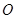 的两条直线
的两条直线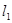 和
和 ,
,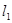 与
与 分别交于
分别交于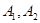 两点,
两点, 与
与 分别交于
分别交于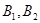 两点.
两点.(1)证明:

(2)过原点
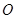 作直线
作直线 (异于
(异于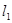 ,
, )与
)与 分别交于
分别交于 两点.记
两点.记 与
与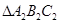 的面积分别为
的面积分别为 与
与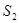 ,求
,求 的值.
的值.
(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)要证明两直线平行,可以利用直线
 的方程
的方程 与抛物线联立,得出
与抛物线联立,得出 ,
, ,
, ,
, ,证明
,证明 ,则
,则 ∥
∥ .;(2)因为
.;(2)因为 ∥
∥ ,同理可得
,同理可得 ∥
∥ ,
, ∥
∥ .由
.由 .因此
.因此 ,由(1)中的
,由(1)中的 知
知 .故
.故 .
.(1)证:设直线
 的方程分别为
的方程分别为 ,则
,则由
 ,得
,得 ,
,由
 ,得
,得 .
.同理可得
 ,
,
所以
 ,
,
故
 ,所以
,所以 ∥
∥ .
.(2)解:由(Ⅰ)知
 ∥
∥ ,同理可得
,同理可得 ∥
∥ ,
, ∥
∥ .
.所以
 .因此
.因此 .又由(1)中的
.又由(1)中的 知
知 .
.故
 .
.
练习册系列答案
相关题目
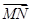 =2
=2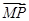 ,
,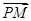 ⊥
⊥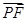 ,当点P在y轴上运动时,点N的轨迹方程为( )
,当点P在y轴上运动时,点N的轨迹方程为( )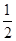 x
x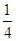 x
x 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于 ,
, 两点.求证:
两点.求证: 为定值;
为定值; 为定值.
为定值.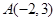 在抛物线C:
在抛物线C: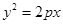 的准线上,记C的焦点为F,则直线AF的斜率为( )
的准线上,记C的焦点为F,则直线AF的斜率为( )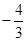
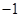
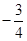
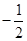
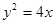 ,直线
,直线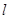 的方程为
的方程为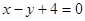 ,在抛物线上有一动点P到y轴的距离为
,在抛物线上有一动点P到y轴的距离为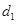 ,P到直线
,P到直线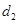 ,则
,则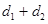 的最小值为( )
的最小值为( ) 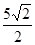


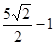
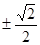
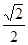
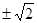
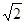
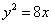 上到其焦点
上到其焦点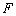 距离为5的点有( )
距离为5的点有( )