题目内容
已知过抛物线 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于 ,
, 两点.求证:
两点.求证:
(1) 为定值;
为定值;
(2) 为定值.
为定值.
 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于 ,
, 两点.求证:
两点.求证:(1)
 为定值;
为定值;(2)
 为定值.
为定值.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)设过焦点
 的直线方程与
的直线方程与 联立,利用韦达定理,即可得出结论;
联立,利用韦达定理,即可得出结论;(2)利用
 ,
, 及根与系数的关系即可得出.
及根与系数的关系即可得出.(1)抛物线
 的焦点为
的焦点为 ,设直线
,设直线 的方程为
的方程为 .
.由
 消去
消去 ,得
,得 .
.由根与系数的关系,得
 (定值).
(定值).当
 轴时,
轴时, ,
, ,也成立.
,也成立.(2)由抛物线的定义,知
 ,
, .
. (定值).
(定值).当
 轴时,
轴时,
 ,上式仍成立.
,上式仍成立.
练习册系列答案
相关题目
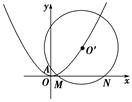
 的焦点为
的焦点为 ,
, 为
为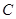 上异于原点的任意一点,过点
上异于原点的任意一点,过点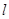 交
交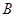 ,交
,交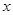 轴的正半轴于点
轴的正半轴于点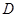 ,且有
,且有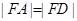 .当点
.当点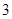 时,
时,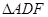 为正三角形.
为正三角形.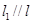 ,且
,且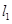 和
和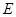 ,
,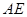 过定点,并求出定点坐标;
过定点,并求出定点坐标;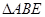 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.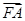 +
+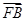 +
+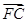 =0,则|
=0,则|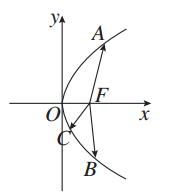
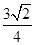 ,则点A的坐标为( )
,则点A的坐标为( )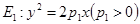 和
和 ,过原点
,过原点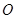 的两条直线
的两条直线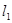 和
和 ,
, 分别交于
分别交于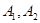 两点,
两点,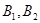 两点.
两点.
 (异于
(异于 两点.记
两点.记 与
与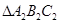 的面积分别为
的面积分别为 与
与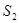 ,求
,求 的值.
的值.