题目内容
如果4sin
+3cos
=0，那么角θ的终边所在的象限是（ ）
| θ |
| 2 |
| θ |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：任意角的三角函数的定义
专题：三角函数的求值
分析：由4sin
+3cos
=0得tan
，进一步求出sinθ和cosθ，由它们的符号来判断θ的终边所在象限．
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
解答：
解：由4sin
+3cos
=0，得tan
=-
∴sinθ=
＜0，
cosθ=
＞0．
∴θ的终边所在象限是第四象限．
故选：D．
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| 3 |
| 4 |
∴sinθ=
2tan
| ||
1+tan2
|
cosθ=
1-tan2
| ||
1+tan2
|
∴θ的终边所在象限是第四象限．
故选：D．
点评：三角函数值符号的确定，可以利用定义、利用三角函数的值的符号、利用象限、利用三角函数线、利用终边相同等方法．
练习册系列答案
相关题目
已知复数z=
，则z对应的点所在的象限是（ ）
| -2+4i |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
用反证法证明命题“设a，b为实数，则方程x2+ax+b=0至少有一个实根”时，要做的假设是（ ）
| A、方程x2+ax+b=0没有实根 |
| B、方程x2+ax+b=0至多有一个实根 |
| C、方程x2+ax+b=0至多有两个实根 |
| D、方程x2+ax+b=0恰好有两个实根 |
椭圆C：
+
=1的左、右顶点分别为M、N，点P在C上，且直线PN的斜率为-
，则直线PM斜率为（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| 4 |
A、
| ||
| B、3 | ||
C、-
| ||
| D、-3 |
已知三条直线m、n、l，三个平面α、β、γ，下列四个命题中，正确的是（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
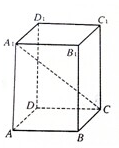如图所示，四棱柱ABCD-A1B1C1D1中，底面ABCD为正方形，高A1A=3，体积为24，则对角线A1C为