题目内容
【题目】已知抛物线![]() :
:![]() 上一点
上一点![]() 到焦点的距离为4,动直线
到焦点的距离为4,动直线![]() 交抛物线
交抛物线![]() 于坐标原点O和点A,交抛物线
于坐标原点O和点A,交抛物线![]() 的准线于点B,若动点P满足
的准线于点B,若动点P满足![]() ,动点P的轨迹C的方程为
,动点P的轨迹C的方程为![]() .
.
(1)求出抛物线![]() 的标准方程;
的标准方程;
(2)求动点P的轨迹方程![]() ;
;
(3)以下给出曲线C的四个方面的性质,请你选择其中的三个方面进行研究:①对称性;②范围;③渐近线;④![]() 时,写出由
时,写出由![]() 确定的函数
确定的函数![]() 的单调区间.
的单调区间.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)根据抛物线上的点到焦点的距离等于到准线的距离列式求解即可.
(2)求出![]() 的坐标,利用动点P满足
的坐标,利用动点P满足![]() ,求出动点P的轨迹C的方程即可.
,求出动点P的轨迹C的方程即可.
(3)根据(2)中所得的方程直接得出结论即可.
(1)由题意,![]() ,所以
,所以![]()
所以抛物线![]() 的标准方程为
的标准方程为![]()
(2)设![]() ,则
,则![]() 与抛物线方程
与抛物线方程![]() 联立,可得
联立,可得![]() ,即
,即![]() ,与
,与![]() 联立,可得
联立,可得![]() .因为
.因为![]() ,所以
,所以![]() ,所以
,所以![]() ,故
,故![]() ,
,![]() .
.
消去![]() 可得
可得![]()
(3)由![]() ,可得
,可得
①因为![]() ,
,![]() ,故
,故![]() 关于
关于![]() 轴对称;
轴对称;
②范围:![]() ,则
,则![]() .即
.即![]()
又当![]() 时,
时, ![]() ,
,
故![]() ,即
,即![]() 或
或![]() .
.
故![]() ,
,![]()
③因为分母为![]() ,故渐近线
,故渐近线![]()
④当![]() 时,因为
时,因为![]() ,所以由
,所以由![]() 确定的函数
确定的函数![]() 为
为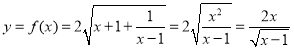 ,即
,即![]()
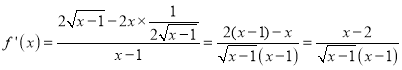 ,
,
当![]() 时
时![]() ,
,![]() 单调递减;当
单调递减;当![]() 时
时![]() ,
,![]() 单调递增
单调递增
故![]() 在
在![]() 上递减,在
上递减,在![]() 上递增.
上递增.
综上所述,
①![]() 关于
关于![]() 轴对称
轴对称
②![]() ,
,![]()
③渐近线![]()
④![]() 时,由
时,由![]() 确定的函数
确定的函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
【题目】某企业生产甲、乙两种产品均需要![]() ,
,![]() 两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
甲 | 乙 | 原料限额 | |
| 3 | 2 | 10 |
| 1 | 2 | 6 |
A. 10万元B. 12万元C. 13万元D. 14万元