题目内容
【题目】已知抛物线![]() 的焦点
的焦点![]() ,
,![]() 上一点坐标为
上一点坐标为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过![]() 作直线
作直线![]() ,交抛物线
,交抛物线![]() 于
于![]() ,
,![]() 两点,若直线
两点,若直线![]() 中点的纵坐标为
中点的纵坐标为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)将点坐标代入解析式,求得![]() 的值,即可求得抛物线方程.
的值,即可求得抛物线方程.
(2)方法一:设点![]() ,
,![]() ,根据中点纵坐标即可利用点差法求得直线的斜率,由点斜式即可求得直线方程;方法二,设出直线方程,联立直线方程与抛物线方程,根据韦达定理和中点的纵坐标,即可求得直线方程.
,根据中点纵坐标即可利用点差法求得直线的斜率,由点斜式即可求得直线方程;方法二,设出直线方程,联立直线方程与抛物线方程,根据韦达定理和中点的纵坐标,即可求得直线方程.
(1)把![]() 代入抛物线方程
代入抛物线方程
解得![]()
∴![]() 的方程为
的方程为![]() .
.
(2)法一:由(1)得抛物线![]() 的方程为
的方程为![]() ,焦点
,焦点![]()
设![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,代入抛物线可得
,代入抛物线可得
则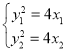 ,两式相减,整理得
,两式相减,整理得![]()
∵线段![]() 中点的纵坐标为
中点的纵坐标为![]()
∴直线![]() 的斜率
的斜率![]()
直线![]() 的方程为
的方程为![]() 即
即![]()
法二:由(1)得抛物线![]() 的方程为
的方程为![]() ,焦点
,焦点![]()
设直线![]() 的方程为
的方程为![]()
由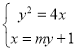 消去
消去![]() ,得
,得![]()
设![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,
,
∵线段![]() 中点的纵坐标为
中点的纵坐标为![]()
∴![]()
解得![]()
直线![]() 的方程为
的方程为![]() 即
即![]()

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
【题目】2018年![]() 年月某市邮政快递业务量完成件数较2017年月
年月某市邮政快递业务量完成件数较2017年月![]() 月同比增长
月同比增长![]() ,如图为该市2017年
,如图为该市2017年![]() 月邮政快递业务量柱状图及2018年
月邮政快递业务量柱状图及2018年![]() 月邮政快递业务量饼图,根据统计图,解决下列问题
月邮政快递业务量饼图,根据统计图,解决下列问题

![]() 年
年![]() 月该市邮政快递同城业务量完成件数与2017年
月该市邮政快递同城业务量完成件数与2017年![]() 月相比是有所增大还是有所减少,并计算,2018年
月相比是有所增大还是有所减少,并计算,2018年![]() 月该市邮政快递国际及港澳台业务量同比增长率;
月该市邮政快递国际及港澳台业务量同比增长率;
![]() 若年平均每件快递的盈利如表所示:
若年平均每件快递的盈利如表所示:
快递类型 | 同城 | 异地 | 国际及港澳台 |
盈利 |
| 5 | 25 |
估计该市邮政快递在2018年![]() 月的盈利是多少?
月的盈利是多少?