Question

已知矩形ABCD，如图所示．长AB=a,宽AD=b，矩形EFGH为其外接矩形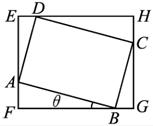．(1)求矩形EFGH面积的最大值；

(2)求矩形EFGH对角线长的最大值；

(3)两个矩形的对角线哪个更长，试证明．

Answer 1

解：

(1)设∠ABF=θ,0°＜θ＜90°,

则由三角形知识可知BF=acosθ,BG=bsinθ,AF=asinθ,AE=bcosθ.

则S_矩形EFGH=EF·EG=(AE+AF)·(BF+BG)

=(asinθ+bcosθ)(acosθ+bsinθ)=a²sinθcosθ+b²sinθcosθ+absin²θ+abcos²θ

=(a²+b²)sin2θ+ab≤ab+(a²+b²)

= (a+b)².

当且仅当sin2θ=1,即θ=时取得最大值. 即矩形EFGH面积的最大值为(a+b)².

(2)矩形EFGH的对角线为EG，EG=

==a+b.

当且仅当θ=时取得最大值.

故矩形EFGH的对角线最大值为a+b.?

(3)EG=＞=AC.故矩形EFGH的对角线更长.