题目内容
(本小题12分)已知数列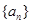 中,
中,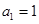 ,且点
,且点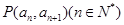 在直线
在直线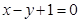 上.
上.
(1) 求数列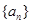 的通项公式;
的通项公式;
(2) 若函数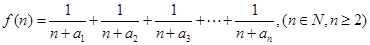 ,求证
,求证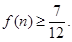
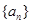 中,
中,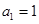 ,且点
,且点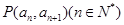 在直线
在直线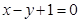 上.
上. (1) 求数列
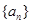 的通项公式;
的通项公式;(2) 若函数
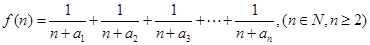 ,求证
,求证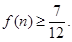
(1)  。(2)见解析。
。(2)见解析。
 。(2)见解析。
。(2)见解析。本试题主要是考查了等差数列的通项公式的运用以及数列求和的综合运用。
(1)由点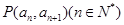 在直线
在直线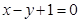 上,即
上,即 ,又
,又 ,
,
 数列
数列 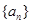 是以1为首项,1 为公差的等差数列
是以1为首项,1 为公差的等差数列 .
.
(2)因为 而
而
 ,可知函数单调性饿到结论。
,可知函数单调性饿到结论。
解:(1)由点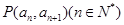 在直线
在直线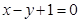 上,即
上,即 ,又
,又 ,
,
 数列
数列 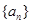 是以1为首项,1 为公差的等差数列
是以1为首项,1 为公差的等差数列 .
.
(2)


 是单调递增,故
是单调递增,故 的最小值是
的最小值是 ,
,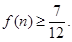
(1)由点
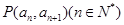 在直线
在直线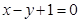 上,即
上,即 ,又
,又 ,
, 数列
数列 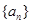 是以1为首项,1 为公差的等差数列
是以1为首项,1 为公差的等差数列 .
.(2)因为
 而
而
 ,可知函数单调性饿到结论。
,可知函数单调性饿到结论。解:(1)由点
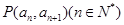 在直线
在直线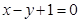 上,即
上,即 ,又
,又 ,
, 数列
数列 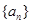 是以1为首项,1 为公差的等差数列
是以1为首项,1 为公差的等差数列 .
.(2)



 是单调递增,故
是单调递增,故 的最小值是
的最小值是 ,
,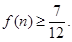

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
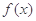 定义在区间
定义在区间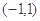 上,
上,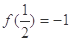 ,且当
,且当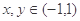 时,恒有
时,恒有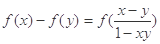 .又数列
.又数列 满足
满足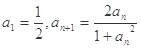 .
.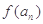 的表达式;
的表达式;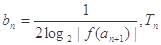 为数列
为数列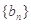 的前
的前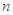 项和,若
项和,若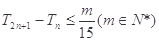 对
对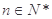 恒成立,求
恒成立,求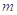 的最小值.
的最小值. 满足:
满足: ,
, ,
, 为公差为4等差数列.数列
为公差为4等差数列.数列 的前n项和为
的前n项和为 ,且满足
,且满足  .
.
 的通项公式
的通项公式 ;
;  的值,使得数列
的值,使得数列 是等差数列;
是等差数列; 满足:
满足:
 与
与 之间插
之间插 个数组成一个公差为
个数组成一个公差为 的等差数列.
的等差数列.  ……
…… 。
。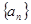 的各项都为正数,其前
的各项都为正数,其前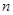 项和为
项和为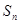 ,已知对任意
,已知对任意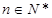 ,
,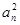 和
和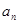 的等差中项.
的等差中项.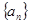 的通项公式;
的通项公式;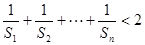 .
.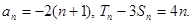
 ,求dn;
,求dn;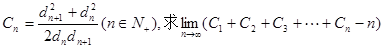 的值.
的值. 的前
的前 项和为
项和为 ,已知
,已知 ,
, 和公差
和公差 的值;
的值; ,求
,求 的前
的前 项和记为
项和记为 ,已知
,已知 .
. ;
; ,求数列
,求数列 的前
的前 .
. ,等比中项是
,等比中项是 ,则曲线
,则曲线 的离心率为( )
的离心率为( ) B.
B. C.
C. D.
D. B.
B. C.
C. D.
D.
 中,
中, ,则
,则 .
.