题目内容
某班从6名班干部(其中男生4人,女生2人)中选3人参加学校学生会的干部竞选.
(1)设所选3人中女生人数为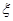 ,求
,求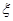 的分布列及数学期望;
的分布列及数学期望;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率.
(1)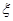 的分布列为
的分布列为
∴ 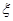
0 1 2 



 。
。
(2)
解析试题分析:解:(1)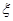 的所有可能取值为0,1,2.
的所有可能取值为0,1,2.
依题意,得 ,
,  ,
,  .
.
∴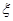 的分布列为
的分布列为
∴ 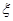
0 1 2 



 。 7分
。 7分
(2)设“男生甲被选中”为事件 ,“女生乙被选中”为事件
,“女生乙被选中”为事件 ,
,
则 ,
, ,
,
∴ .
.
故在男生甲被选中的情况下,女生乙也被选中的概率为 . 12分
. 12分
考点:随机变量的分布列
点评:主要是考查了随机变量的分布列和期望值的运用,属于基础题。

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
为普及高中生安全逃生知识与安全防护能力,某学校高一年级举办了高中生安全知识与安全逃生能力竞赛. 该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛.先将所有参赛选手参加笔试的成绩(得分均为整数,满分为 分)进行统计,制成如下频率分布表.
分)进行统计,制成如下频率分布表.
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 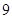 |  |
| [70,80) | 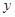 |  |
| [80,90) | 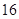 | 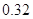 |
| [90,100) |  |  |
| 合 计 | 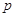 |  |
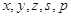 的值;
的值;(Ⅱ)按规定,预赛成绩不低于
 分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.
分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.①求决赛出场的顺序中,甲不在第一位、乙不在最后一位的概率;
②记高一·二班在决赛中进入前三名的人数为
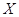 ,求
,求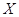 的分布列和数学期望.
的分布列和数学期望. 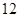 名工人,随机抽取
名工人,随机抽取 名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数. 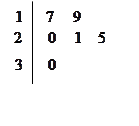
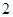 人,求恰有
人,求恰有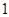 名优秀工人的概率.
名优秀工人的概率.  为选出的4个学生中女生的人数,求
为选出的4个学生中女生的人数,求 ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是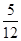 ,得到黄球或绿球的概率是
,得到黄球或绿球的概率是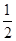 ,试求得到黑球、黄球、绿球的概率各是多少?
,试求得到黑球、黄球、绿球的概率各是多少?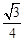 );
);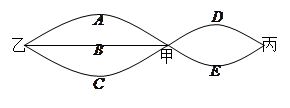
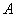 、
、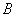 、
、 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是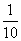 ,
, 、
、 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.
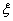 表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求
表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求