题目内容
设T={（x，y）|ax+y-3=0}，S={（x，y）|x-y-b=0}．若S∩T={（2，1）}，则a•b=
1
1
．分析：由题意可知（2，1）在直线ax+y-3=0与x-y-b=0即可求出a，b然后得到a•b的值．
解答：解：T={（x，y）|ax+y-3=0}，S={（x，y）|x-y-b=0}．若S∩T={（2，1）}，
所以（2，1）在直线ax+y-3=0与x-y-b=0，所以a=1，b=1，
所以a•b=1．
故答案为：1．
所以（2，1）在直线ax+y-3=0与x-y-b=0，所以a=1，b=1，
所以a•b=1．
故答案为：1．
点评：本题考查集合的基本运算，集合元素的属性，直线的交点的求法，考查计算能力．
练习册系列答案
相关题目
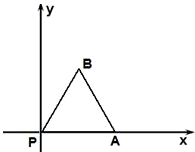如图，放置的边长为1的正三角形PAB沿 x轴滚动．设顶点P（x，y）的纵坐标与横坐标的函数关系式是y=f（x），记f（x）的最小正周期为T；y=f（x）在其两个相邻零点间的图象与x轴所围区域的面积记为S，则S•T=
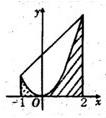如图，设T是直线x=-1，x=2与函数y=x2的图象在x轴上方围成的直角梯形区域，S是T内函数y=x2图象下方的点构成的区域（图中阴影部分）．向T中随机投一点，则该点落入S中的概率为（ ）
如图放置的边长为1的正方形PABC沿x轴滚动．设顶点p（x，y）的轨迹方程是y=f（x），设f（x）的最小正周期为T，y=f（x）在其两个相邻零点间的图象与x轴所围区域的面积为S，则ST=
如图放置的边长为1的正方形PABC沿x轴滚动（向右为顺时针，向左为逆时针）．设顶点p（x，y）的轨迹方程是y=f（x），则关于f（x）的最小正周期T及y=f（x）在其两个相邻零点间的图象与x轴所围区域的面积S的正确结论是（ ）