题目内容
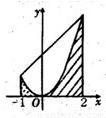
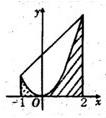 如图,设T是直线x=-1,x=2与函数y=x2的图象在x轴上方围成的直角梯形区域,S是T内函数y=x2图象下方的点构成的区域(图中阴影部分).向T中随机投一点,则该点落入S中的概率为( )
如图,设T是直线x=-1,x=2与函数y=x2的图象在x轴上方围成的直角梯形区域,S是T内函数y=x2图象下方的点构成的区域(图中阴影部分).向T中随机投一点,则该点落入S中的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:本题利用几何概型求解.欲求恰好落在阴影范围内的概率,只须求出阴影范围内的面积与梯形的面积比即可.
解答:解:∵梯形的面积为
(1+4)×3=
,
阴影部分的面积为:
S=∫
2 dx=
x3|
=3,
∴落在阴影范围内的概率
P=
=
.
故选B
| 1 |
| 2 |
| 15 |
| 2 |
阴影部分的面积为:
S=∫
2 -1 |
| 1 |
| 3 |
2 -1 |
∴落在阴影范围内的概率
P=
| 3 | ||
|
| 2 |
| 5 |
故选B
点评:本题主要考查了几何概型.如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.

练习册系列答案
相关题目
A.选修4-1:几何证明选讲
|
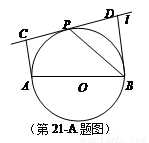
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.求证:(1)l是⊙O的切线;(2)PB平分∠ABD.
B.选修4-2:矩阵与变换
(本小题满分10分)
已知点A在变换:T:→=作用后,再绕原点逆时针旋转90°,得到点B.若点B坐标为(-3,4),求点A的坐标.
C.选修4-4:坐标系与参数方程
(本小题满分10分)
求曲线C1:被直线l:y=x-所截得的线段长.
D.选修4-5:不等式选讲
(本小题满分10分)
已知a、b、c是正实数,求证:≥.
 已知椭圆E:
已知椭圆E: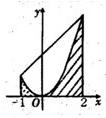 如图,设T是直线x=-1,x=2与函数y=x2的图象在x轴上方围成的直角梯形区域,S是T内函数y=x2图象下方的点构成的区域(图中阴影部分).向T中随机投一点,则该点落入S中的概率为
如图,设T是直线x=-1,x=2与函数y=x2的图象在x轴上方围成的直角梯形区域,S是T内函数y=x2图象下方的点构成的区域(图中阴影部分).向T中随机投一点,则该点落入S中的概率为