题目内容
【题目】若关于x的方程22x+2xa+a+1=0有实根,求实数a的取值范围.
【答案】解:法一:(换元法)
设t=2x(t>0),则原方程可变为t2+at+a+1=0,(*)
原方程有实根,即方程(*)有正根.
令f(t)=t2+at+a+1.
①若方程(*)有两个正实根t1 , t2 ,
则 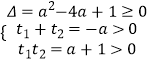 解得-1<a≤2-2
解得-1<a≤2-2 ![]() ;
;
②若方程(*)有一个正实根和一个负实根(负实根,不合题意,舍去),则f(0)=a+1<0,解得a<-1;
③当a=-1时,t=1,x=0符合题意.
综上可知实数a的取值范围是(-∞,2-2 ![]() ].
].
法二:(分离变量法)
由方程,解得a=- ![]() ,设t=2x(t>0),
,设t=2x(t>0),
则a=- ![]() =-
=- ![]()
=2- ![]() ,其中t+1>1,
,其中t+1>1,
由基本(均值)不等式,得(t+1)+ ![]() ≥2
≥2 ![]() ,当且仅当t=
,当且仅当t= ![]() -1时取等号,故a≤2-2
-1时取等号,故a≤2-2 ![]() .
.
综上可知实数a的取值范围是(-∞,2-2 ![]() ].
].
【解析】先换元,令t=2x , 则关于 t 方程为t2+at+a+1=0 有实根,令![]() ,结合基本不等式即可解出实数m的取值范围.或者用分离参数,利用基本不等式,即可求得实数m的取值范围.
,结合基本不等式即可解出实数m的取值范围.或者用分离参数,利用基本不等式,即可求得实数m的取值范围.

练习册系列答案
相关题目