题目内容
(本小题满分12分)
已知函数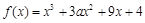 在
在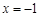 时有极值.
时有极值.
(Ⅰ)求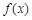 的解析式;
的解析式;
(Ⅱ)求函数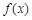 在
在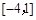 上的最大值、最小值.
上的最大值、最小值.
已知函数
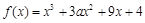 在
在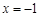 时有极值.
时有极值.(Ⅰ)求
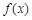 的解析式;
的解析式;(Ⅱ)求函数
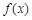 在
在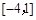 上的最大值、最小值.
上的最大值、最小值.解析:(Ⅰ) .
.  ;
;
(Ⅱ) ,
, .
.
 .
.  ;
;(Ⅱ)
 ,
, .
.本试题主要是考查了导数在研究汗珠中的运用。
(1)根据给定某点的极值可知该点的导数值为零,然后得到参数的值,得到解析式。
(2)根据导数来结合导数的符号判定函数的单调性,得到单调区间进而得到最值。
解:(Ⅰ) ,由题知
,由题知 ,
, ,得
,得 .
.
∴ 6分
6分
(Ⅱ) , 8分
, 8分
则方程 有根
有根 或
或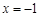 .
.
10分
 ,
, ,而
,而 ,
,
 ,
, . 12分
. 12分
(1)根据给定某点的极值可知该点的导数值为零,然后得到参数的值,得到解析式。
(2)根据导数来结合导数的符号判定函数的单调性,得到单调区间进而得到最值。
解:(Ⅰ)
 ,由题知
,由题知 ,
, ,得
,得 .
. ∴
 6分
6分(Ⅱ)
 , 8分
, 8分则方程
 有根
有根 或
或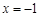 .
.| x |  |  |  |  |  |
 | + | 0 | - | 0 | + |
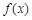 | 增 | 极大值 | 减 | 极小值 | 增 |
 ,
, ,而
,而 ,
, ,
, . 12分
. 12分
练习册系列答案
相关题目
 在
在 内有极小值,则实数
内有极小值,则实数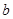 的取值范围
的取值范围  在
在 及
及 时取得极值.
时取得极值. ,都有
,都有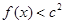 成立,求c的取值范围(6分)
成立,求c的取值范围(6分)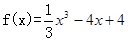 在
在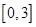 上的最大值是( )
上的最大值是( )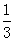
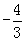
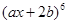 的展开式中
的展开式中 与
与 的系数之比为
的系数之比为 ,其中
,其中
 时,求
时,求 ,求
,求 的最小值.
的最小值. 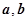 满足:
满足: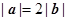 ,若函数
,若函数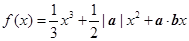 在
在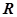 上有极值,设向量
上有极值,设向量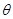 ,则
,则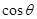 的取值范围为( )
的取值范围为( )
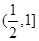


 在闭区间 [– 3,0] 上的最大值、最小值分别是( )
在闭区间 [– 3,0] 上的最大值、最小值分别是( )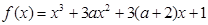 有极大值和极小值,则
有极大值和极小值,则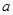 的取值范围是__________.
的取值范围是__________. 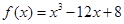 在区间
在区间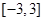 上的最大值与最小值分别为
上的最大值与最小值分别为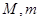 ,则
,则 .
.