题目内容
2013年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
|
组别 |
PM2.5浓度 (微克/立方米) |
频数(天) |
频率 |
|
第一组 |
(0,25] |
5 |
0.25 |
|
第二组 |
(25,50] |
10 |
0.5 |
|
第三组 |
(50,75] |
3 |
0.15 |
|
第四组 |
(75,100) |
2 |
0.1 |
(Ⅰ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(Ⅱ)求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
(1)0.6
(2)该居民区的环境需要改进
【解析】
试题分析:(Ⅰ) 设PM2.5的24小时平均浓度在(50,75]内的三天记为 ,PM2.5的24小时平均浓度在(75,100)内的两天记为
,PM2.5的24小时平均浓度在(75,100)内的两天记为 .
.
所以5天任取2天的情况有: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, 共10种.
4分
共10种.
4分
其中符合条件的有:
 ,
, ,
, ,
, ,
, ,
, 共6种. 6分
共6种. 6分
所以所求的概率 .
8分
.
8分
(Ⅱ)去年该居民区PM2.5年平均浓度为: (微克/立方米). 10分
(微克/立方米). 10分
因为 ,所以去年该居民区PM2.5年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进.
12分
,所以去年该居民区PM2.5年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进.
12分
考点:频率分布表、古典概型
点评:本小题主要考查频率分布表、古典概型、统计等基础知识,考查数据处理能力、运算求解能力以及应用意识,考查必然与或然思想等

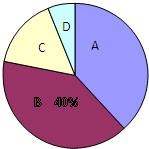 2013年4月9日至14日,西安市共有35000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
2013年4月9日至14日,西安市共有35000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表: