题目内容
16.不等式(x-1)$•\sqrt{{x}^{2}-x-2}$≥0的解集为[2,+∞)∪{-1}.分析 求出不等式的等价形式,解得即可.
解答 解:不等式(x-1)$•\sqrt{{x}^{2}-x-2}$≥0,等价为:$\left\{\begin{array}{l}{{x}^{2}-x-2>0}\\{x-1≥0}\end{array}\right.$或x2-x-2=0,x>2或x=2或x=-1,
故答案为:[2,+∞)∪{-1}.
点评 本题考查无理不等式的解法,容易出错处是x2-x-2=0,是基础题.

练习册系列答案
相关题目
6.假设坐标平面上一非空集合S内的点(x,y),具有以下性质:“若x>0.则y>0”,试问下列哪个叙述对S内的点(x,y)必定成立( )
| A. | 若x≤0,则y≤0 | B. | 若y≤0,则x≤0 | C. | 若y>0,则x>0 | D. | 若y>0,则x≤0 |
7.已知集合M={f(x)|f(x)=$\frac{1}{\sqrt{1-x}}$},N={g(x)|g(x)=ln(x+1)},则M∩N=( )
| A. | (1,1) | B. | (0,+∞) | C. | (1,+∞) | D. | (-∞,1) |
11.y=2x-1的定义域是( )
| A. | (-∞,+∞) | B. | (1,+∞) | C. | [1,+∞) | D. | (0,1)∪(1,+∞) |
8.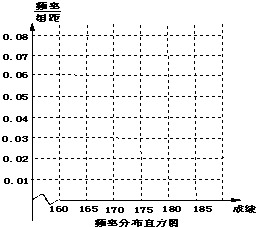 某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)由(1)所做频率分布直方图,估测出这100名学生成绩的众数、中位数、平均数;
(3)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
 某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)由(1)所做频率分布直方图,估测出这100名学生成绩的众数、中位数、平均数;
(3)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [160,165) | 5 | 0.050 |
| 第2组 | [165,170) | ① | 0.350 |
| 第3组 | [170,175) | 30 | ② |
| 第4组 | [175,180) | 20 | 0.200 |
| 第5组 | [180,185] | 10 | 0.100 |
| 合计 | 100 | 1.00 | |
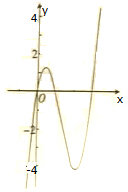 已知函数f(x)=2x(x-1)(x-3)的图象如图所示,有以下关于方程f(x)+1=0的说法:①有2个实数根;②当x>0时,有1个实数根;③当-1<x<0时,有1个实数根;④当x>1时,有1个实数根;⑤当-1<x<3时,有3个实数根.其中正确说法的序号是③⑤(填上所有正确命题的序号).
已知函数f(x)=2x(x-1)(x-3)的图象如图所示,有以下关于方程f(x)+1=0的说法:①有2个实数根;②当x>0时,有1个实数根;③当-1<x<0时,有1个实数根;④当x>1时,有1个实数根;⑤当-1<x<3时,有3个实数根.其中正确说法的序号是③⑤(填上所有正确命题的序号).