Question

【题目】长度为的AB在光滑水平面上转动，同时以速度滑动，离棒的中心距离处有一竖直墙。要使棒平着与墙相撞（如图所示），

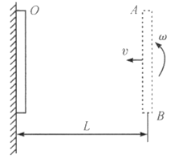
试问：棒的角速度应为多少；若设以此时AB为x轴，并设A为x轴的起点O，求碰前瞬间棒上离A点距离为x的任意点速度的函数表示式。

Answer 1

【答案】当时， ；当时， ； 当时，

【解析】

显然,要使棒平着与墙相撞,历时,此时,转过的角度应满足
。
同时,与墙相撞时,下端的速度应满足
，
即.所以，棒的角速度应为

，，。
所以,碰前瞬间棒上离A点距离为x的任意点速度的函数表示式满足:
①当时,有
，
②当时,有
，
③当时，有

本题中要满足“棒平着与墙相撞”的条件有两个,显性条件容易确定,而隐性条件则不易挖掘,这一条件也是满足要求的临界条件。
临界条件在各种问题中都有可能出现,平时要多加练习,掌握其分析要领,避免出错。