Question

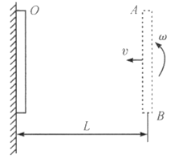
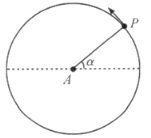
【题目】如图所示，轻绳的一端固定在A点，另一端系一小球。当小球沿圆周逆时针方向运动到P点，绳子恰好松弛，此时轻绳与水平方向的夹角满足关系：，求小球从P点运动至最高点所需的时间，与绳子保持松弛的时间的比值。

Answer 1

【答案】

【解析】

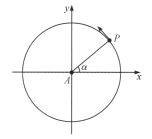
建立如图所示的坐标系,设小球在P点的速度为v，绳长为l，由绳子恰好松弛，有

，即。

绳子松弛后,小球做抛体运动,以后有

，，

，

。

小球从P点运动至最高点时，，所需的时间满足

。

当绳子再次绷紧时，有，即

。

将代入并整理得

，

即，所以，。

对于抛体运动,轨迹约束条件(多数是几何条件)的确定与二次方程的求解是这类试题的两大障碍,学习者如能认识到这一点,就应该明确了努力的方向,多加练习、归纳,临场时也就更容易突破障碍了。