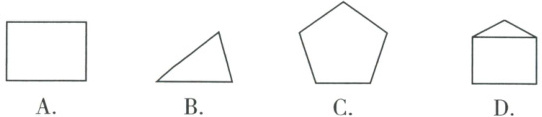
1. 下列图形中,具有稳定性的是(
B
).
答案:B
解析:
三角形具有稳定性,四边形及多边形不具有稳定性。选项A是四边形,B是三角形,C是五边形,D是组合图形(含四边形),故具有稳定性的是B。
2. 已知下列各组中三条线段的长度,其中不能组成三角形的是(
A.2 cm,3 cm,4 cm
B.3 cm,6 cm,6 cm
C.2 cm,2 cm,6 cm
D.5 cm,6 cm,7 cm
C
).A.2 cm,3 cm,4 cm
B.3 cm,6 cm,6 cm
C.2 cm,2 cm,6 cm
D.5 cm,6 cm,7 cm
答案:C
解析:
要判断三条线段能否组成三角形,需满足三角形两边之和大于第三边的条件。
对选项逐一验证:
A. 2 + 3 > 4,2 + 4 > 3,3 + 4 > 2,满足条件;
B. 3 + 6 > 6,3 + 6 > 6,6 + 6 > 3,满足条件;
C. 2 + 2 < 6(不满足),因此不能组成三角形;
D. 5 + 6 > 7,5 + 7 > 6,6 + 7 > 5,满足条件。
对选项逐一验证:
A. 2 + 3 > 4,2 + 4 > 3,3 + 4 > 2,满足条件;
B. 3 + 6 > 6,3 + 6 > 6,6 + 6 > 3,满足条件;
C. 2 + 2 < 6(不满足),因此不能组成三角形;
D. 5 + 6 > 7,5 + 7 > 6,6 + 7 > 5,满足条件。
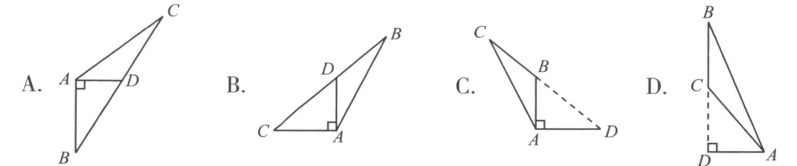
3. 下面四个图形中,线段$AD$是$\triangle ABC$中边$BC$上的高的图形为(
C
).
答案:C
解析:
根据三角形高的定义,过顶点A向对边BC所在直线作垂线,垂足为D,则AD是BC边上的高。选项C中,AD垂直于BC,垂足为D,符合定义。
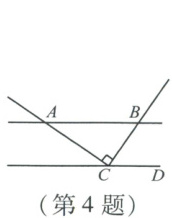
4. 如图,直线$AB// CD$,且$AC\perp BC$于点$C$.若$\angle BAC = 35^{\circ}$,则$\angle BCD$的度数为(
A.$65^{\circ}$
B.$55^{\circ}$
C.$45^{\circ}$
D.$35^{\circ}$
B
).
A.$65^{\circ}$
B.$55^{\circ}$
C.$45^{\circ}$
D.$35^{\circ}$
答案:B
解析:
∵AC⊥BC,∴∠ACB=90°。
在Rt△ABC中,∠BAC=35°,
∴∠ABC=90°-∠BAC=90°-35°=55°。
∵AB//CD,
∴∠BCD=∠ABC=55°(两直线平行,内错角相等)。
5. 若$a$,$b$,$c$为$\triangle ABC$的三边,且$a$,$b$满足$\sqrt{a - 3} + (b - 2)^2 = 0$,第三边$c$是整数,则$c$的值可以是(
A.1
B.3
C.5
D.7
B
).A.1
B.3
C.5
D.7
答案:B
解析:
由$\sqrt{a - 3} + (b - 2)^2 = 0$,得$a-3=0$,$b-2=0$,所以$a=3$,$b=2$。根据三角形三边关系,$3-2 < c < 3+2$,即$1 < c < 5$。因为$c$是整数,所以$c=2,3,4$,选项中符合的是3。
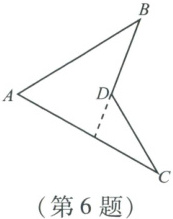
6. 如图,若$\angle A = 70^{\circ}$,$\angle B = 40^{\circ}$,$\angle C = 32^{\circ}$,则$\angle BDC =$ (
A.$102^{\circ}$
B.$110^{\circ}$
C.$142^{\circ}$
D.$148^{\circ}$
C
).
A.$102^{\circ}$
B.$110^{\circ}$
C.$142^{\circ}$
D.$148^{\circ}$
答案:C
解析:
连接AD并延长至点E。根据三角形外角性质,∠BDE=∠BAD+∠B,∠CDE=∠CAD+∠C。则∠BDC=∠BDE+∠CDE=∠BAD+∠B+∠CAD+∠C=(∠BAD+∠CAD)+∠B+∠C=∠A+∠B+∠C。已知∠A=70°,∠B=40°,∠C=32°,故∠BDC=70°+40°+32°=142°。
7. 已知一个等腰三角形的两条边长分别为$4 cm$和$6 cm$,则它的周长为(
A.$14 cm$
B.$16 cm$
C.$14 cm$或$16 cm$
D.不能确定
C
).A.$14 cm$
B.$16 cm$
C.$14 cm$或$16 cm$
D.不能确定
答案:C
解析:
若$4cm$为腰长,则三角形的三边长度分别为$4cm$,$4cm$,$6cm$,满足三角形三边关系(任意两边之和大于第三边),此时周长为 $4 + 4 + 6 = 14(cm)$。
若$6cm$为腰长,则三角形的三边长度分别为$6cm$,$6cm$,$4cm$,也满足三角形三边关系,此时周长为 $6 + 6 + 4 = 16(cm)$。
所以,等腰三角形的周长有两种可能,$14cm$或$16cm$。
若$6cm$为腰长,则三角形的三边长度分别为$6cm$,$6cm$,$4cm$,也满足三角形三边关系,此时周长为 $6 + 6 + 4 = 16(cm)$。
所以,等腰三角形的周长有两种可能,$14cm$或$16cm$。
8. 如图,$AD$,$BE$,$CF$是$\triangle ABC$的三条中线,则下列说法中错误的是(
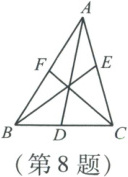
A.$AE = \frac{1}{2}AC$
B.$AB = 2BF$
C.$AD = CF$
D.$BD = DC$
C
).
A.$AE = \frac{1}{2}AC$
B.$AB = 2BF$
C.$AD = CF$
D.$BD = DC$
答案:C
解析:
由题意知,$AD$、$BE$和$CF$是$\triangle ABC$的三条中线,
根据中线的性质,中线将对边分成两等份。
对于选项$AE = \frac{1}{2}AC$,因为$E$是$AC$的中点,所以该选项正确。
对于选项$AB = 2BF$,因为$F$是$AB$的中点,所以该选项正确。
对于选项$BD = DC$,因为$D$是$BC$的中点,所以该选项正确。
对于选项$AD = CF$,没有理由表明一条中线等于另一条中线,所以该选项错误。
根据中线的性质,中线将对边分成两等份。
对于选项$AE = \frac{1}{2}AC$,因为$E$是$AC$的中点,所以该选项正确。
对于选项$AB = 2BF$,因为$F$是$AB$的中点,所以该选项正确。
对于选项$BD = DC$,因为$D$是$BC$的中点,所以该选项正确。
对于选项$AD = CF$,没有理由表明一条中线等于另一条中线,所以该选项错误。
9. 在$\triangle ABC$中,$\angle A=\angle C$,$CD$平分$\angle ACB$交$AB$于点$D$,$\angle ADC = 150^{\circ}$.设$\angle B$的度数为$x^{\circ}$,列方程可求得$\angle B$的度数为(
A.$150^{\circ}$
B.$140^{\circ}$
C.$130^{\circ}$
D.$120^{\circ}$
B
).A.$150^{\circ}$
B.$140^{\circ}$
C.$130^{\circ}$
D.$120^{\circ}$
答案:B
解析:
设∠A=∠C=y°,∠B=x°。
∵△ABC内角和为180°,∴2y + x = 180°,即y=(180°-x)/2。
∵CD平分∠ACB,∴∠ACD=∠ACB/2=y/2。
在△ADC中,∠A + ∠ADC + ∠ACD=180°,∠ADC=150°,
∴y + 150° + y/2 = 180°,解得(3y)/2=30°,y=20°。
代入y=(180°-x)/2,得20°=(180°-x)/2,解得x=140°。
∵△ABC内角和为180°,∴2y + x = 180°,即y=(180°-x)/2。
∵CD平分∠ACB,∴∠ACD=∠ACB/2=y/2。
在△ADC中,∠A + ∠ADC + ∠ACD=180°,∠ADC=150°,
∴y + 150° + y/2 = 180°,解得(3y)/2=30°,y=20°。
代入y=(180°-x)/2,得20°=(180°-x)/2,解得x=140°。
目录查找(点击展开或折叠章节目录)
切换年代卷册
X
