1. 画圆时,固定的一点叫作
圆心
,常用字母O
表示;从圆心
到圆上
任意一点的线段,叫作半径,常用字母r
表示;通过圆心并且两端都在圆上的线段,叫作直径
,常用字母d
表示。答案:圆心
O
圆心
圆上
r
直径
d
O
圆心
圆上
r
直径
d
解析:
本题主要考查圆的基本概念,包括圆心、半径和直径的定义及其表示方法。
1. 画圆时,固定的一点叫作圆心,这是圆定义的基础,它决定了圆的位置。圆心常用字母O表示。
2. 从圆心到圆上任意一点的线段,叫作半径。半径是圆的一个重要参数,它决定了圆的大小。半径常用字母r表示。
3. 通过圆心并且两端都在圆上的线段,叫作直径。直径是半径的两倍,也是圆的一个重要参数。直径常用字母d表示。
1. 画圆时,固定的一点叫作圆心,这是圆定义的基础,它决定了圆的位置。圆心常用字母O表示。
2. 从圆心到圆上任意一点的线段,叫作半径。半径是圆的一个重要参数,它决定了圆的大小。半径常用字母r表示。
3. 通过圆心并且两端都在圆上的线段,叫作直径。直径是半径的两倍,也是圆的一个重要参数。直径常用字母d表示。
2. 画圆时,(
圆心
)确定圆的位置,(半径
)决定圆的大小。答案:圆心
半径
半径
解析:
在画圆的过程中,圆心的位置决定了圆在平面上的位置,而半径的长度则决定了圆的大小。
3. 在一个圆里可以画出(
无数
)条半径,(无数
)条直径。答案:无数
无数
无数
解析:
连接圆心和圆上任意一点的线段叫做半径,圆上有无数个点,所以可以画出无数条半径;通过圆心并且两端都在圆上的线段叫做直径,同样圆上有无数个点,过圆心可以画出无数条直径。
4. 如果要画一个直径为 5cm 的圆,那么圆规两脚间的距离应为(
2.5
)cm。答案:2.5
解析:
画圆时,圆规两脚间的距离是圆的半径。已知圆的直径为5cm,半径等于直径的一半,即5÷2=2.5cm,所以圆规两脚间的距离应为2.5cm。
5. 下面的线段是相应圆的半径或直径的画√,并标上相应的字母。

( ) ( ) ( ) (

( ) ( ) ( ) (
√d
) (√r
) ( )答案:d
r
√
√
r
√
√
解析:
根据半径是连接圆心和圆上任意一点的线段,直径是通过圆心并且两端都在圆上的线段。第一个图线段两端在圆上且过圆心,是直径,标d;第二个图线段一端圆心一端圆上,是半径,标r;第三个图线段一端圆心一端圆上,是半径,标r;第四个图线段一端圆心一端圆上,是半径,标r;第五个图线段不过圆心,不是半径或直径;第六个图线段两端在圆上且过圆心,是直径,标d。
6. (1) 以点 O 为圆心,画一个直径是 2cm 的圆。
(2) 画一个半径是 1.5cm 的圆,并标上 O,r,d。
(2) 画一个半径是 1.5cm 的圆,并标上 O,r,d。
答案:
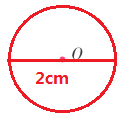
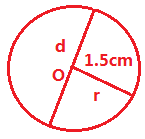


解析:
(1)以点 O 为圆心,1cm 为半径画圆。
(2)以点 O 为圆心,1.5cm 为半径画圆,标出圆心 O,半径 r=1.5cm,直径 d=3cm。
(2)以点 O 为圆心,1.5cm 为半径画圆,标出圆心 O,半径 r=1.5cm,直径 d=3cm。
7. 写出下列各图中圆的半径和直径的长度。



3cm
6cm
8cm
16cm

2cm
4cm
答案:3cm
8cm
6cm
16cm
2cm
4cm
8cm
6cm
16cm
2cm
4cm
解析:
第一个图:圆的直径等于正方形边长6cm,半径r=6÷2=3cm,d=6cm;第二个图:两个半圆直径和等于正方形边长16cm,一个半圆直径d=16cm,半径r=16÷2=8cm;第三个图:小圆直径2cm,大圆半径等于小圆直径2cm,直径d=2×2=4cm。
8. 右图中大圆的半径为 8cm,小圆的半径为 3.5cm,求线段 $ O_1O_2 $ 的长。


答案:
∵ 大圆半径 $R = 8 cm$,小圆半径 $r = 3.5 cm$,
∴ $O_1O_2 = R - r = 8 cm - 3.5 cm = 4.5 cm$。
∴线段$O_1O_2$的长为$4.5cm$。
∵ 大圆半径 $R = 8 cm$,小圆半径 $r = 3.5 cm$,
∴ $O_1O_2 = R - r = 8 cm - 3.5 cm = 4.5 cm$。
∴线段$O_1O_2$的长为$4.5cm$。
9. 把一个圆的半径扩大到原来的 2 倍,那么圆的直径扩大到原来的(
$ O_1O_2 $长(
2
)倍。$ O_1O_2 $长(
4.5
)cm。答案:2
4.5
4.5
解析:
因为圆的直径$d = 2r$,当半径$r$扩大到原来的2倍时,新直径$d' = 2×(2r) = 4r = 2×(2r) = 2d$,所以直径扩大到原来的2倍。题目中未给出关于$O_1O_2$的相关图形或数据信息,无法计算其长度,此处可能存在题目信息缺失。
目录查找(点击展开或折叠章节目录)
切换年代卷册
X
