1. 填空。
(1)圆中心的一点叫作
(2)连接圆心和圆上任意一点的线段叫作
(3)通过圆心并且两端都在圆上的线段叫作
(4)在同一个圆内,直径的长度是半径的
(5)
(6)经过一点可以画
(1)圆中心的一点叫作
圆心
,用字母O
表示,它到圆上任意一点的距离都相等
。(2)连接圆心和圆上任意一点的线段叫作
半径
,用字母r
表示。(3)通过圆心并且两端都在圆上的线段叫作
直径
,用字母d
表示。(4)在同一个圆内,直径的长度是半径的
2
倍。(5)
圆心
确定圆的位置,半径
确定圆的大小。(6)经过一点可以画
无数
个圆。答案:圆心
O
相等
半径
r
直径
d
2
圆心
半径
无数
O
相等
半径
r
直径
d
2
圆心
半径
无数
解析:
(1) 圆中心的一点叫作圆心,这是圆的基本定义,用字母$O$表示。圆心到圆上任意一点的距离是相等的,这是圆的基本性质。
(2) 连接圆心和圆上任意一点的线段叫作半径,这是半径的定义,用字母$r$表示。
(3) 通过圆心并且两端都在圆上的线段叫作直径,这是直径的定义,用字母$d$表示。
(4) 在同一个圆内,直径的长度是半径的两倍,这是由圆的性质决定的。
(5) 圆心确定圆的位置,因为圆心是圆的中心点,它的位置决定了圆的位置。半径确定圆的大小,因为半径决定了圆上任意一点到圆心的距离,从而决定了圆的大小。
(6) 经过一点可以画无数个圆,因为只要固定这一点作为圆心,然后选择不同的半径长度,就可以画出不同的圆。
(2) 连接圆心和圆上任意一点的线段叫作半径,这是半径的定义,用字母$r$表示。
(3) 通过圆心并且两端都在圆上的线段叫作直径,这是直径的定义,用字母$d$表示。
(4) 在同一个圆内,直径的长度是半径的两倍,这是由圆的性质决定的。
(5) 圆心确定圆的位置,因为圆心是圆的中心点,它的位置决定了圆的位置。半径确定圆的大小,因为半径决定了圆上任意一点到圆心的距离,从而决定了圆的大小。
(6) 经过一点可以画无数个圆,因为只要固定这一点作为圆心,然后选择不同的半径长度,就可以画出不同的圆。
2. 判断,正确的打"√",错误的打"×"。
(1)圆的半径都相等。(
(2)两端都在圆上的线段一定是直径。(
(3)2个半圆可以拼成一个整圆。(
(4)直径是圆内最长的线段。(
(5)画一个直径4厘米的圆,圆规两脚应叉开4厘米。(
(6)直径都是半径的2倍。(
(1)圆的半径都相等。(
×
)(2)两端都在圆上的线段一定是直径。(
×
)(3)2个半圆可以拼成一个整圆。(
×
)(4)直径是圆内最长的线段。(
√
)(5)画一个直径4厘米的圆,圆规两脚应叉开4厘米。(
×
)(6)直径都是半径的2倍。(
×
)答案:×
×
×
√
×
×
×
×
√
×
×
解析:
(1) 圆的半径是圆心到圆上任意一点的距离,只有在同一个圆或等圆中,所有的半径才相等。因此,此题说法错误。
(2) 直径是穿过圆心的特殊弦,两端都在圆上且经过圆心的线段才是直径。所以,此题说法错误。
(3) 只有两个完全相同的半圆才能拼成一个整圆,如果两个半圆的半径不同,则无法拼成一个整圆。此题说法错误。
(4) 在圆内,任何一条从圆心到圆上的线段(即半径)都会比不过圆心的线段(即弦)要长,而直径是经过圆心的特殊弦,因此直径是圆内最长的线段。此题说法正确。
(5) 画圆时,圆规两脚叉开的距离应为圆的半径,而不是直径。所以,如果要画一个直径4厘米的圆,圆规两脚应叉开2厘米,而不是4厘米。此题说法错误。
(6) 在同一个圆中,直径确实是半径的2倍。但此题没有指明是在同一个圆中,因此此题说法错误。
(2) 直径是穿过圆心的特殊弦,两端都在圆上且经过圆心的线段才是直径。所以,此题说法错误。
(3) 只有两个完全相同的半圆才能拼成一个整圆,如果两个半圆的半径不同,则无法拼成一个整圆。此题说法错误。
(4) 在圆内,任何一条从圆心到圆上的线段(即半径)都会比不过圆心的线段(即弦)要长,而直径是经过圆心的特殊弦,因此直径是圆内最长的线段。此题说法正确。
(5) 画圆时,圆规两脚叉开的距离应为圆的半径,而不是直径。所以,如果要画一个直径4厘米的圆,圆规两脚应叉开2厘米,而不是4厘米。此题说法错误。
(6) 在同一个圆中,直径确实是半径的2倍。但此题没有指明是在同一个圆中,因此此题说法错误。
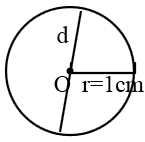
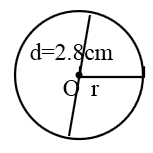
3. 用圆规画圆,并用字母O、r、d分别标出它的圆心、半径和直径。
(1)半径是1厘米。
(2)直径是2.8厘米。
(1)半径是1厘米。
(2)直径是2.8厘米。
答案:


4. 想一想,填一填。

圆的直径:

圆的直径:
6
dm;正方形的边长:6
dm。答案:6
6
6
解析:
从图中可以看出,圆的半径是3分米。
圆的直径是半径的2倍,所以圆的直径为$3×2=6$分米。
图中正方形的边长等于圆的直径,所以正方形的边长也是6分米。
圆的直径是半径的2倍,所以圆的直径为$3×2=6$分米。
图中正方形的边长等于圆的直径,所以正方形的边长也是6分米。
5. 你想怎么研究正六边形?
答案:可以通过以下步骤研究正六边形:
1. 观察正六边形的形状,确定它有六条边和六个内角。
2. 使用尺子测量正六边形的各边长度,会发现所有边长度相等。
3. 使用量角器测量正六边形的各个内角,会发现每个内角都是$120^\circ$。
4. 研究正六边形的对称性,可以发现它有六条对称轴,分别是经过对边中点的直线和经过对角顶点的直线。
5. 尝试用圆规和直尺作出正六边形,方法是以一定长度为半径画圆,再用圆规依次截取圆上等距的六个点,最后依次连接这些点。
结论:正六边形六条边长度相等,六个内角均为$120^\circ$,有六条对称轴,可以用圆规和直尺作出。
1. 观察正六边形的形状,确定它有六条边和六个内角。
2. 使用尺子测量正六边形的各边长度,会发现所有边长度相等。
3. 使用量角器测量正六边形的各个内角,会发现每个内角都是$120^\circ$。
4. 研究正六边形的对称性,可以发现它有六条对称轴,分别是经过对边中点的直线和经过对角顶点的直线。
5. 尝试用圆规和直尺作出正六边形,方法是以一定长度为半径画圆,再用圆规依次截取圆上等距的六个点,最后依次连接这些点。
结论:正六边形六条边长度相等,六个内角均为$120^\circ$,有六条对称轴,可以用圆规和直尺作出。
目录查找(点击展开或折叠章节目录)
切换年代卷册
X
