14. 如图所示,电源电压保持18V不变,小灯泡L上标有“6V 3W”字样,滑动变阻器最大电阻值R=60Ω.为保证各器件安全,不考虑灯丝电阻随温度的变化,下列说法正确的是( )
如图所示,电源电压保持18V不变,小灯泡L上标有“6V 3W”字样,滑动变阻器最大电阻值R=60Ω.为保证各器件安全,不考虑灯丝电阻随温度的变化,下列说法正确的是( )
 如图所示,电源电压保持18V不变,小灯泡L上标有“6V 3W”字样,滑动变阻器最大电阻值R=60Ω.为保证各器件安全,不考虑灯丝电阻随温度的变化,下列说法正确的是( )
如图所示,电源电压保持18V不变,小灯泡L上标有“6V 3W”字样,滑动变阻器最大电阻值R=60Ω.为保证各器件安全,不考虑灯丝电阻随温度的变化,下列说法正确的是( )| A. | S断开时电压表示数为0V | |
| B. | S闭合后,电压表最大示数为15V | |
| C. | 小灯泡L正常发光时,变阻器R消耗的电功率为6W | |
| D. | S闭合后,小灯泡L的最小实际电功率为0.75W |
13. 在底面积相同的甲、乙两个容器中,装入质量相等的液体放在水平桌面上,小球A、B体积相等,如图所示.分别将小球A放在甲容器中,将小球B放入乙容器中,小球均悬浮.下列说法正确的是( )
在底面积相同的甲、乙两个容器中,装入质量相等的液体放在水平桌面上,小球A、B体积相等,如图所示.分别将小球A放在甲容器中,将小球B放入乙容器中,小球均悬浮.下列说法正确的是( )
 在底面积相同的甲、乙两个容器中,装入质量相等的液体放在水平桌面上,小球A、B体积相等,如图所示.分别将小球A放在甲容器中,将小球B放入乙容器中,小球均悬浮.下列说法正确的是( )
在底面积相同的甲、乙两个容器中,装入质量相等的液体放在水平桌面上,小球A、B体积相等,如图所示.分别将小球A放在甲容器中,将小球B放入乙容器中,小球均悬浮.下列说法正确的是( )| A. | 两容器中不放小球时,甲、乙两容器底受到的压强相等 | |
| B. | 甲容器中的液体密度比乙容器中的液体密度大 | |
| C. | 小球B在乙容器中受到的浮力大 | |
| D. | 小球A在甲容器中受到的浮力大于小球B在乙容器中受到的浮力 |
10.下列说法正确的是( )
| A. | 海市蜃楼是光的反射现象 | |
| B. | 人离平面镜越远,平面镜所成的像越小 | |
| C. | 听众能根据音调来辨别乐器 | |
| D. | “禁鸣”是从声源处减弱噪音 |
5.演绎式探究
演绎式探究--原子内部电子绕原子核的运动
0 166651 166659 166665 166669 166675 166677 166681 166687 166689 166695 166701 166705 166707 166711 166717 166719 166725 166729 166731 166735 166737 166741 166743 166745 166746 166747 166749 166750 166751 166753 166755 166759 166761 166765 166767 166771 166777 166779 166785 166789 166791 166795 166801 166807 166809 166815 166819 166821 166827 166831 166837 166845 235360
演绎式探究--原子内部电子绕原子核的运动
| (1)我们知道,原子有原子核和核外电子组成,核外电子绕原子核高速旋转.按照波尔理论,电子绕原子核做匀速圆周运动,且电子会受到原子核的静电吸引力(如图甲).已知,电子受到的静电吸引力F电与原子序数Z成正比,与元电荷e的平方成正比,与电子运动的轨道半径r的平方的关系如右图乙图象所示,k是静电常数.则电子所受的静电吸引力的数学表达式为:B. A.${F_电}=\frac{{Z{e^2}{r^2}}}{4πk}$B.${F_电}=\frac{{Z{e^2}}}{{4πk{r^2}}}$C.${F_电}=\frac{e^2}{{4πkZ{r^2}}}$D.${F_电}=\frac{{Z{r^2}}}{{4πk{e^2}}}$ 其中静电常数k=8.85×10-12,当物体做匀速圆周运动时,必须受到一个向圆心拉的力,这个力叫做向心力,电子绕原子核做匀速圆周运动的向心力${F_心}=m\frac{υ^2}{r}$,其中m为电子的质量,υ为电子的运动速度.且电子做圆周运动的向心力等于电子受到的静电吸引力. (2)波尔引用量子理论,提出电子运动的轨道不是任意的,轨道数n从内向外依次为1、2、3、…,(如图丙)并且提出$mυr=n\frac{h}{2π}$,其中n为轨道数,h为常数,h=6.63×10-34J•s.请推导出电子的轨道速度υ的数学表达式. (3)已知氧原子的原子序数Z=8,元电荷e=1.6×10-19C,求氧原子中电子在轨道数n=2的轨道上运动式的速度υ2= 8.73×106m/s. | 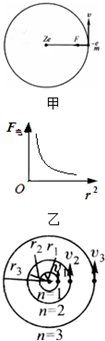 |
 适当进行足浴对身体很有好处,如图所示是小澜同学给奶奶买的家用电热足浴盆,其加热电功率为1000W,最大容水量是5L,自重5kg,限定最高温度是50℃,盆与地面的接触面积是8cm2.已知水的比热容是4.2×l03J/(kg•℃),g取10N/kg.求:
适当进行足浴对身体很有好处,如图所示是小澜同学给奶奶买的家用电热足浴盆,其加热电功率为1000W,最大容水量是5L,自重5kg,限定最高温度是50℃,盆与地面的接触面积是8cm2.已知水的比热容是4.2×l03J/(kg•℃),g取10N/kg.求: 实验室中的电压表一般是由小量程的电流计G与某一电阻串联后改装而成,如图甲所示,在测量中电压表的示数即为其两端的电压.
实验室中的电压表一般是由小量程的电流计G与某一电阻串联后改装而成,如图甲所示,在测量中电压表的示数即为其两端的电压.
 如图所示,是小轿车汽油机工作时的能量转化示意图,消耗2kg汽油,可获得的动能是多少?(汽油的热值为4.6×107J/kg)
如图所示,是小轿车汽油机工作时的能量转化示意图,消耗2kg汽油,可获得的动能是多少?(汽油的热值为4.6×107J/kg)