题目内容
8.甲乙两辆汽车沿平直公路同方向驶向山洞,当距山1710m时,两车头恰好平齐,甲车鸣笛一声.甲车司机经T1时间听到山反射回来的回声,从鸣笛到听到回声甲车行进了S1,乙车司机经T2时间听到回声,从鸣笛到听到回声乙车行进S2,已知S1:S2=19:36,T1比T2多$\frac{1}{2}$s秒,声速为340m/s,若甲车长20m,乙车长30m,问甲车的速度是多少?甲车司机看乙车从他身边错过需多少s?分析 (1)声音传播的距离与车行驶的距离之差为听到回声时车距高山距离的2倍,由速度公式的变形公式分别表示出分析S1、S2;然后根据已知S1:S2=19:36,T1比T2多$\frac{1}{2}$s秒求出两辆汽车的速度;
(2)甲车司机看乙车从他身边错过时需要的时间相同,但乙车需要多通过的路程为两车的长度,利用s=vt根据路程关系求出需要的时间.
解答 解:(1)由v=$\frac{s}{t}$得:
甲车鸣笛后经T1时间行驶距离:s1=v甲T1=2s-v声T1,
乙车鸣笛后经T2时间行驶距离:s2=v乙T2=2s-v声T2,
由于s1:s2=19:36,
则(2×s-v声T1):(2×s-v声T2)=19:36,
即:(2×1710m-340m/s×T1):(2×1710m-340m/s×T2)=19:36----------①
已知T1-T2=$\frac{1}{2}$s-----------②
解①②得:T1=9.5s,T2=9s;
根据s1=v甲T1=2s-v声T1得:
v甲=$\frac{2s}{{T}_{1}}$-v声=$\frac{2×1710m}{9.5s}$-340m/s=20m/s;
根据s2=v乙T2=2s-v声T2得:
v乙=$\frac{2s}{{T}_{2}}$-v声=$\frac{2×1710m}{9s}$-340m/s=40m/s;
(2)设甲车司机看乙车从他身边错过需时间为t′,
则通过的路程关系为:v乙t′=v甲t′+L乙,
所以,t′=$\frac{{L}_{乙}}{{v}_{乙}-{v}_{甲}}$=$\frac{30m}{40m/s-20m/s}$=1.5s.
答:甲车的速度是40m/s;甲车司机看乙车从他身边错过需1.5s.
点评 本题考查的是学生对速度计算公式的理解和掌握,弄清楚距离关系是解决此题的关键.

| 实验序号 | 时刻 | 海拔高度h(米) | 大气压强p(厘米汞高) |
| 1 | 8:00 | 0 | 75.2 |
| 2 | 10:00 | 0 | 75.3 |
| 3 | 12:00 | 0 | 75.0 |
| 4 | 12:00 | 120 | 74.0 |
| 5 | 12:00 | 240 | 73.0 |
| 6 | 12:00 | 360 | 72.0 |
| 7 | 12:00 | 480 | 71.0 |
(2)该小组同学分析实验序号3、4、5、6、7,发现同一时刻大气压的值和海拔高度的数值之间存在一定的数量关系,从现有数据可以退出P和h的数量关系时p=133×(75-$\frac{h}{120}$)帕(用h的代数式表示).
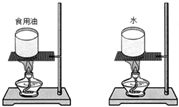 为了比较水和食用油的某种特性,小明用两个相同的装置做了如图所示的实验.用温度计测量液体吸收热量后升高的温度值,并用钟表记录加热时间.实验数据记录如表.
为了比较水和食用油的某种特性,小明用两个相同的装置做了如图所示的实验.用温度计测量液体吸收热量后升高的温度值,并用钟表记录加热时间.实验数据记录如表.| 物质 | 质量/g | 初始温度/℃ | 加热时间/min | 最后温度/℃ |
| 水 | 60 | 20 | 6 | 45 |
| 食用油 | 60 | 20 | 6 | 68 |
(2)在此实验中,如果要使水和食用油的最后温度相同,就要给水加热更长的时间,此时水吸收的热量大于(选填“大于”或“小于”或“等于”)食用油吸收的热量.
(3)通过实验可以得到不同的物质吸热能力不同,物质的这种特性用比热容这个物理量来描述.
 小程同学分别测量了三块橡皮泥的质量和体积,并根据测量数据画出如图所示的图象,由图象可知:橡皮泥的密度是2g/cm3;橡皮泥的质量和体积具有正比关系.
小程同学分别测量了三块橡皮泥的质量和体积,并根据测量数据画出如图所示的图象,由图象可知:橡皮泥的密度是2g/cm3;橡皮泥的质量和体积具有正比关系. 如图,是一种无绳电水壶的铭牌.某同学用这种电水壶烧水,他将水放至最大水量,测得水的温度是18℃,通电5min,水烧开(标准大气压下),试通过计算,回答下列问题:此水壶正常工作时的电流是多大?该电水壶电热丝的电阻是多少?若测得电源电压实际为210V,算一算此电水壶工作的功率是多大?
如图,是一种无绳电水壶的铭牌.某同学用这种电水壶烧水,他将水放至最大水量,测得水的温度是18℃,通电5min,水烧开(标准大气压下),试通过计算,回答下列问题:此水壶正常工作时的电流是多大?该电水壶电热丝的电阻是多少?若测得电源电压实际为210V,算一算此电水壶工作的功率是多大? 小明同学做“比较两种材料的保温性能”的实验,根据实验测得的数据,绘制了下面表示“水温与时间关系”的图象.实验过程中室温保持不变.
小明同学做“比较两种材料的保温性能”的实验,根据实验测得的数据,绘制了下面表示“水温与时间关系”的图象.实验过程中室温保持不变.