题目内容
某人用绳子将一物体从水面下2m深处的地方匀速提到水面下0.5m处的过程中,所用时间为6s,拉力F1做功的功率为9W,当物体拉到有l/5的体积露出水面时,让其静止,此时绳子对物体的拉力为40N,不计绳子的质量,忽略水的阻力.求:(1)拉力F1的大小;(2)物体浸没时所受的浮力;(3)物体的密度.
分析:(1)求出物体在水面下上升的距离,知道所用时间,利用速度公式求物体的上升速度;知道拉力做功功率,再利用P=
=
=Fv求拉力F1的大小;
(2)当物体全浸没时,物体受到的浮力F浮=ρ水v排g=ρ水v物g,而F浮+F1=G;
当物体
露出水面(
浸没水中)时,物体受到的浮力F浮′=ρ水
v物g,而F浮′+F2=G;联立方程组求解;
(3)求出了物体完全浸没时受到的浮力,利用阿基米德原理F浮=ρ水v排g求物体的体积;利用F浮+F1=G求物体重,利用重力公式G=mg求物体的质量,再用密度公式ρ=
求物体的密度.
| W |
| t |
| Fs |
| t |
(2)当物体全浸没时,物体受到的浮力F浮=ρ水v排g=ρ水v物g,而F浮+F1=G;
当物体
| 1 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
(3)求出了物体完全浸没时受到的浮力,利用阿基米德原理F浮=ρ水v排g求物体的体积;利用F浮+F1=G求物体重,利用重力公式G=mg求物体的质量,再用密度公式ρ=
| m |
| v |
解答:解:(1)物体在水下上升的距离:
s=2m-0.5m=1.5m,
上升速度:
v=
=
=0.25m/s,
∵P=
=
=Fv,P=9W,
∴拉力F1的大小:
F1=
=
=36N;
(2)当物体浸没时,F1=G-F浮=G-ρ水v排g=G-ρ水v物g=,----------①
当物体有
体积露出水面时:F2=G-F浮′=G-
ρ水v物g=G-
F浮---------②
由①②式得到:
F浮=F2-F1,
F浮=5(F2-F1)=5×(40N-36N)=20N;
(3)当物体浸没时,F浮=20N,G=F1+F浮=36N+20N=56N,
∵F浮=ρ水v排g=ρ水v物g,
∴v物=
=
=2×10-3m3,
物体的质量:
m=
=
=5.6kg,
物体的密度:
ρ物=
=
=2.8×103kg/m3.
答:(1)拉力F1的大小为36N;
(2)物体浸没时所受的浮力20N;
(3)物体的密度为2.8×103kg/m3.
s=2m-0.5m=1.5m,
上升速度:
v=
| s |
| t |
| 1.5m |
| 6s |
∵P=
| W |
| t |
| Fs |
| t |
∴拉力F1的大小:
F1=
| P |
| v |
| 9W |
| 0.25m/s |
(2)当物体浸没时,F1=G-F浮=G-ρ水v排g=G-ρ水v物g=,----------①
当物体有
| 1 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
由①②式得到:
| 1 |
| 5 |
F浮=5(F2-F1)=5×(40N-36N)=20N;
(3)当物体浸没时,F浮=20N,G=F1+F浮=36N+20N=56N,
∵F浮=ρ水v排g=ρ水v物g,
∴v物=
| F浮 |
| ρ水g |
| 20N |
| 1×103kg/m3×10N/kg |
物体的质量:
m=
| G |
| g |
| 56N |
| 10N/kg |
物体的密度:
ρ物=
| m |
| v物 |
| 5.6kg |
| 2×10-3m3 |
答:(1)拉力F1的大小为36N;
(2)物体浸没时所受的浮力20N;
(3)物体的密度为2.8×103kg/m3.
点评:本题考查了重力的公式、密度的公式、阿基米德原理及推导公式、功率公式、速度公式,知识点多、综合性强,属于难题!

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
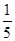 体积露出水面时,让其静止,此时绳子对物体的拉力为40N.不计绳子的质量,忽略水的阻力,求物体的密度.(g取10N/kg)
体积露出水面时,让其静止,此时绳子对物体的拉力为40N.不计绳子的质量,忽略水的阻力,求物体的密度.(g取10N/kg)