题目内容
17.如图1所示.将两个实心金属块挂在杠杆上,杠杆在水平位置平衡.若实心金属块分别为铜块和铁块,分析下列情况并回答问题:(1)若两个金属块同时向外、或者同时向里移动相同的距离.杠杠将会怎样?
(2)若将两个金属块各增加或减少相同的质量,杠杠将会怎样?
(3)若两个金属块质量相等,均为实心,一个是铜质的,一个是铁质的,杠杆等臂,若两金属块均浸没在水中,杠杠将会怎样?

(4)若甲、乙均为某材质的金属块,其密度为ρ=2.6×103kg/m3,体积之比为13:2.若甲浸没在水中平衡时,乙刚好在B点;若甲浸没在某液体中平衡时,乙在C点,OC:OA=2:1,求OA:OB和ρ液.
(5)若甲和乙是由不同物质构成的实心金属块.甲为立方体,静止在地面上;杠杠AB水平平衡.已知:OA=30cm,AB=75cm,现将支点O移动5cm后,甲对地面的压强变为零;已知:甲边长L甲=20 cm,乙体积V乙=1dm3,ρ甲:ρ乙=1:4.
(6)[接题(5)]OA=30cm,甲、乙两物体挂在杠杆两端,且杠杆水平平衡;若把乙浸没在水中,杠杠仍处于平衡.此时,甲对地的压强发生变化.则△p甲375Pa (g取10 N/kg)
分析 (1)由图可知杠杆水平平衡以及两者力臂之间的关系,根据杠杆的平衡条件可知它们的重力关系,然后判断两个金属块同时向外、或者同时向里移动相同的距离时力与力臂乘积的变化关系,然后根据力和力臂乘积大的下沉、乘积小的会上翘判断杠杆转动的方向;
(2)将两个金属块各增加或减少相同的质量时重力的变化量相同,然后判断力与力臂乘积的变化关系,然后根据力和力臂乘积大的下沉、乘积小的会上翘判断杠杆转动的方向;
(3)铜的质量大于铁的质量,根据密度公式判断两实心球的体积关系,根据阿基米德原理判断两球受到浮力之间的关系,绳子对杠杆的作用力等于重力减去受到的浮力,然后得出作用力和力臂乘积之间的关系,最后根据力和力臂乘积大的下沉、乘积小的会上翘判断杠杆转动的方向;
(4)根据密度公式和重力公式表示出物体的重力,根据阿基米德原理表示出甲浸没在水中时受到的浮力,甲对杠杆的拉力等于自身的重力减去受到的浮力,利用杠杆平衡条件得出等式即可求出OA:OB,同理求出某液体的密度;
(5)知道甲的边长可求其体积,根据密度公式和重力公式表示出物体的重力,将支点O移动5cm后甲金属块的力臂减小5cm,据此求出两金属块的力臂,此时甲对地面的压强变为零,根据杠杆的平衡条件得出等式即可求出两金属的密度之比;
(6)把乙浸没在水中,根据阿基米德原理求出乙受到的浮力,根据杠杆的平衡条件得出乙浸没在水中前后甲物体的拉力,两者的差值即为甲对地面压力的变化量,根据p=$\frac{F}{S}$求出甲对地压强的变化量.
解答 解:(1)由图可知,杠杆水平平衡,且L铜>L铁,
由杠杆的平衡条件可知:G铜•L铜=G铁•L铁,
所以G铜<G铁,
当两个金属块同时向外移动相同的距离△L后,G铜•△L<G铁•△L,
则G铜•(L铜+△L)<G铁•(L铁+△L),
所以,挂铁块的一端下沉,杠杠将会顺时针转动;
同理可知,两个金属块同时向里移动相同的距离△L后,G铜•△L<G铁•△L,
则G铜•(L铜-△L)>G铁•(L铁-△L),
所以,挂铜块的一端下沉,杠杠将会逆时针转动;
(2)当两个金属块各增加相同的质量时,它们增加的重力相同,△G•L铜>△G•L铁,
则(G铜+△G)•L铜>(G铁+△G)•L铁,
所以,挂铜块的一端下沉,杠杠将会逆时针转动;
同理可知,当两个金属块各减少相同的质量时,它们减小的重力相同,△G•L铜>△G•L铁,
则(G铜+△G)•L铜<(G铁+△G)•L铁,
所以,挂铁块的一端下沉,杠杠将会顺时针转动;
(3)由题意可知,实心铜球和铁球的质量相等,且铜的密度大于铁的密度,
由ρ=$\frac{m}{V}$可知,铁球的体积大于铜球的体积,
由F浮=ρgV排可知,两球浸没在水中时,铁球受到的浮力大于铁球受到的浮力,
因两球的质量相等,重力相等,且绳子的拉力等于球的重力减去受到的浮力,
所以,铜球绳子的拉力大于铁球绳子的拉力,
因杠杆是等臂杠杆,
所以,铜球绳子的拉力与力臂的乘积大于铁球绳子的拉力与力臂的乘积,
故铜球一端下沉,杠杠将会逆时针转动;
(4)由ρ=$\frac{m}{V}$和G=mg可得,甲乙两金属块的重力分别为:
G甲=m甲g=ρV甲g,G乙=m乙g=ρV乙g,
甲浸没在水中时受到的浮力F浮=ρ水gV甲,
甲金属块对杠杆的拉力:
F甲=G甲-F浮=ρV甲g-ρ水gV甲=(ρ-ρ水)gV甲,
由杠杆的平衡条件可得:
(ρ-ρ水)gV甲•OA=ρV乙g•OB,
则$\frac{OA}{OB}$=$\frac{ρ{V}_{乙}}{(ρ-{ρ}_{水}){V}_{甲}}$=$\frac{ρ}{ρ-{ρ}_{水}}$×$\frac{{V}_{乙}}{{V}_{甲}}$=$\frac{2.6×1{0}^{3}kg/{m}^{3}}{2.6×1{0}^{3}kg/{m}^{3}-1.0×1{0}^{3}kg/{m}^{3}}$×$\frac{2}{13}$=$\frac{1}{4}$;
若甲浸没在某液体中平衡时,乙在C点,OC:OA=2:1,
甲物体对杠杆的拉力:
F甲′=G甲-F浮′=ρV甲g-ρ液gV甲=(ρ-ρ液)gV甲,
由杠杆的平衡条件可得:
(ρ-ρ液)gV甲•OA=ρV乙g•OC,
则ρ液=(1-$\frac{{V}_{乙}•OC}{{V}_{甲}•OA}$)ρ=(1-$\frac{{V}_{乙}}{{V}_{甲}}$×$\frac{OC}{OA}$)ρ=(1-$\frac{2}{13}$×$\frac{2}{1}$)×2.6×103kg/m3=1.8×103kg/m3;
(5)正方体甲的体积:
V甲=L甲3=(2dm)3=8dm3,
由ρ=$\frac{m}{V}$和G=mg可得,甲乙两金属块的重力分别为:
G甲=m甲g=ρV甲g,G乙=m乙g=ρV乙g,
将支点O移动5cm后,甲对地面的压强变为零,
则OA=30cm-5cm=25cm,OB=75cm-25cm=50cm,
由杠杆的平衡条件可得:
ρ甲gV甲•OA=ρ乙V乙g•OB,
则$\frac{{ρ}_{甲}}{{ρ}_{乙}}$=$\frac{{V}_{乙}•OB}{{V}_{甲}•OA}$=$\frac{1d{m}^{3}×50cm}{8d{m}^{3}×25cm}$=$\frac{1}{4}$;
(5)把乙浸没在水中前,由杠杆的平衡条件可得:
FA•OA=G乙•OB-------------①
把乙浸没在水中后,
FA′•OA=(G乙-F浮)•OB----②
由①②可得,甲对地面压力的变化量:
△FA=$\frac{OB′}{OA′}$F浮=$\frac{OB′}{OA′}$ρ水gV乙=$\frac{45cm}{30cm}$×1.0×103kg/m3×10N/kg×1×10-3m3=15N,
受力面积:
S甲=L甲2=(20cm)2=400cm3=0.04m3,
甲对地压强的变化量:
△p=$\frac{△{F}_{A}}{{S}_{甲}}$=$\frac{15N}{0.04{m}^{3}}$=375Pa.
答:(1)两个金属块同时向外移动相同的距离时杠杆顺时针转动,两个金属块同时向里移动相同的距离时杠杠逆时针转动;
(2)两个金属块各增加相同的质量时杠杠逆时针转动,两个金属块各减少相同的质量时杠杠顺时针转动;
(3)两金属块均浸没在水中后,杠杠将会逆时针转动;
(4)OA:OB的比值为1:4,液体的密度ρ液为1.8×103kg/m3;
(5)1:4;
(6)375.
点评 本题主要考查了杠杆平衡条件的应用,同时用到了浮力、拉力、压强、压力和重力之间的大小关系,是一道综合性题目,需要根据已知条件利用杠杆的平衡条件列关系式,从而得出结论.

 习题精选系列答案
习题精选系列答案
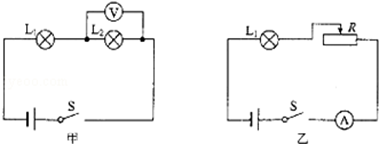
(1)请你用笔画线代替导线,把图甲所示的实验电路补充完整.
(2)小彬把5Ω的定值电阻接入电路后,闭合开关,发现电压表有示数而电流表无示数,则电路中的故障可能是R断路(写出一种);排除故障后,闭合开关,调节滑动变阻器的滑片P,使电流表的示数如图乙所示,此时电路中的电流为0.2 A.
(3)将5Ω定值电阻换成10Ω定值电阻,闭合开关,为了保持电压表的示数不变,应将滑动变阻器的滑片P向A(选填“A”或“B”)移动,记录此时各仪表的示数.
(4)将10Ω定值电阻换成20Ω定值电阻,重复步骤(3).
| 实验次数 | 定值电阻Ω) | 电流表示数(A) |
| 1 | 5 | |
| 2 | 10 | 0.1 |
| 3 | 20 | 0.05 |
(5)该小组用30Ω的电阻替换20Ω的电阻进行了第4次实验,发现实验无法进行下去,为完成第4次实验,同学们提出了下列解决方案,其中正确的是D.
A.将电压表换接另一个量程
B.换成电压为4.5V的电源
C.换成“50Ω 2A”的滑动变阻器
D.可将上述实验中定值电阻两端的电压调为1.5V.
(1)为保证实验的科学性,除了取大小、厚度相同的泡沫塑料和棉絮外,还应考虑影响水温变化的其他因素,即保持烧瓶相同、环境因素相同、水的多少和初温都相同.
(2)按照计划操作,小明与小芳把实验测得的时间和温度数据记录在表中:
| 时间(min) | 0 | 10 | 20 | 30 | 40 | … | 150 | 180 |
| 泡沫塑料组水温(℃) | 90 | 74 | 65 | 60 | 57 | … | 21 | 20 |
| 棉絮组水温(℃) | 90 | 70 | 55 | ? | 33 | … | 20 | 20 |
(3)小明与小芳是采用了“在相同的时间内,比较水温降低多少”的方法来比较两种材料的保温性能的,你还可以采用“降低相同的温度,比较时间长短”的方法来比较两种材料的保温性能.
(4)仔细分析水温变化规律则,时间为30min时,棉絮组的水温可能是下列选项中的哪一个?A
A.42℃B.44℃C.46℃D.48℃
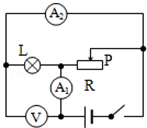
| A. | 灯泡L变亮 | B. | 电压表示数不变 | ||
| C. | 电流表A1示数变大 | D. | 电流表A2示数变大 |
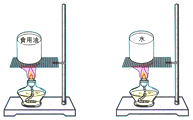 为了比较水和食用油的吸热能力,小明用两个相同的装置做了如图所示的实验.用温度计测量液体吸收热量后升高的温度值,并用钟表记录加热时间.实验数据记录如表.
为了比较水和食用油的吸热能力,小明用两个相同的装置做了如图所示的实验.用温度计测量液体吸收热量后升高的温度值,并用钟表记录加热时间.实验数据记录如表.| 物质 | 质量/g | 初始温度/℃ | 加热时间/min | 最后温度/℃ |
| 水 | 60 | 20 | 6 | 45 |
| 食用油 | 60 | 20 | 6 | 68 |
(2)在此实验中,如果要使水和食用油的最后温度相同,就要给水加热更长的时间,从而看出水的吸热能力大于(选填“大于”或“小于”或“等于”)食用油的吸热能力.
(3)物质的这种特性用比热容这个物理量来描述.

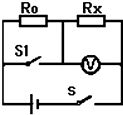 用伏安法测未知电阻R的阻值,若实验中只有一个电压表和一个已知电阻R0,小明设计了如图所示的电路,同样可以测量未知电阻Rx,请在空格内将实验步骤补充完整
用伏安法测未知电阻R的阻值,若实验中只有一个电压表和一个已知电阻R0,小明设计了如图所示的电路,同样可以测量未知电阻Rx,请在空格内将实验步骤补充完整