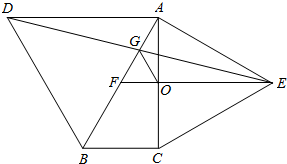
如图.分别以Rt△ABC的斜边AB.直角边AC为边向外作等边△ABD和△ACE.F为AB的中点.连接DF.EF.DE.EF与AC交于点O.DE与AB交于点G.连接OG.若∠BAC=30°.下列结论:①——青夏教育精英家教网——

如图，分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE，F为AB的中点，连接DF、EF、DE，EF与AC交于点O，DE与AB交于点G，连接OG，若∠BAC=30°，下列结论：
①△DBF≌△EFA；②AD=AE；③EF⊥AC；④AD=4AG；⑤△AOG与△EOG的面积比为1：4．
其中正确结论的序号是（　　）

不等式-5x+7＞3x-5的解是（　　）

8、在平面直角坐标系中，点P（-3，2005）在（　　）

A、第一象限

B、第二象限

C、第三象限

D、第四象限

已知：如图，抛物线y=

x2-3x+c交x轴正半轴于A、B两点，交y轴于C点，过A、

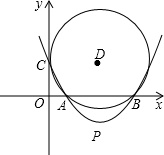B、C三点作⊙D．若⊙D与y轴相切．
（1）求c的值；
（2）连接AC、BC，设∠ACB=α，求tanα；
（3）设抛物线顶点为P，判断直线PA与⊙D的位置关系，并证明．

已知：如图，点N为△ABC的内心，延长AN交BC于点D，交△ABC的外接圆于点E．

（1）求证：EB=EN=EC；
（2）求证：NE²=AE•DE．

在平面直角坐标系中，将抛物线y₁=x²-4x+1向左平移3个单位长度，再向上平移4个单位长度，得到抛物线y₂，然后将抛物线y₂绕其顶点顺时针旋转180°，得到抛物线y₃．
（1）求抛物线y₂、y₃的解析式．
（2）求y₃＜0时，x的取值范围．
（3）判断以抛物线y₃的顶点以及其与x轴的交点为顶点的三角形的形状，并求它的面积．

18、已知抛物线经过两点A（1，0）、B（3，0），且对称轴是直线x=2，求其解析式．

如图，平行四边形ABCD中，AB=10cm，BC=8cm，点E为AD边上一点且DE=5cm，连接CE并延长交BA的延长线于点F．求AF的长．

用一个半径为4 cm，圆心角为120°的扇形纸片围成一个圆锥（接缝处不重叠），求这个圆锥的高．

14、用配方法求抛物线y=-x²-2x+3的顶点坐标．

0 75763 75771 75777 75781 75787 75789 75793 75799 75801 75807 75813 75817 75819 75823 75829 75831 75837 75841 75843 75847 75849 75853 75855 75857 75858 75859 75861 75862 75863 75865 75867 75871 75873 75877 75879 75883 75889 75891 75897 75901 75903 75907 75913 75919 75921 75927 75931 75933 75939 75943 75949 75957 366461