题目内容
已知:如图,抛物线y=| 1 | 2 |
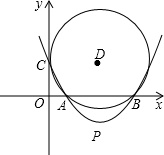 B、C三点作⊙D.若⊙D与y轴相切.
B、C三点作⊙D.若⊙D与y轴相切.(1)求c的值;
(2)连接AC、BC,设∠ACB=α,求tanα;
(3)设抛物线顶点为P,判断直线PA与⊙D的位置关系,并证明.
分析:(1)根据圆和抛物线的对称性可知:圆心D必在抛物线的对称轴上,因此D的横坐标与抛物线的对称轴的值相同,可根据抛物线的解析式求出对称轴的值即可得出D点的横坐标,由于圆D和y轴相切,因此D的横坐标就是圆的半径.先根据抛物线的解析式,用c表示出A、B的坐标,即可表示AB的长,然后在直角三角形AED中,AE=
AB,DE=OC=c,已经求得了圆的半径根据勾股定理即可得出c的值,进而可求出抛物线的解析式.
(2)由于∠ACB不在直角三角形中,因此无法直接求出其正切值,可通过构建直角三角形来求解.延长AD交圆与F,连接BF,那么∠ABF=90°,根据圆周角定理可知:∠F=∠ACB=α,因此在直角三角形ABF中,求∠F的正切值即可.
(3)连接PA,证∠PAD是否等于90°即可,根据抛物线的解析式可得出A、B、P的坐标,然后根据坐标系中两点间的距离公式求出DA2、AP2、DP2的长,看DA2+AP2是否与DP2相等即可.
| 1 |
| 2 |
(2)由于∠ACB不在直角三角形中,因此无法直接求出其正切值,可通过构建直角三角形来求解.延长AD交圆与F,连接BF,那么∠ABF=90°,根据圆周角定理可知:∠F=∠ACB=α,因此在直角三角形ABF中,求∠F的正切值即可.
(3)连接PA,证∠PAD是否等于90°即可,根据抛物线的解析式可得出A、B、P的坐标,然后根据坐标系中两点间的距离公式求出DA2、AP2、DP2的长,看DA2+AP2是否与DP2相等即可.
解答: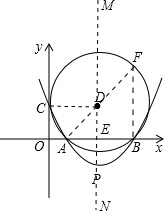 解:(1)连接DC,作AB的垂直平分线MN,交AB于E,连接DA.
解:(1)连接DC,作AB的垂直平分线MN,交AB于E,连接DA.
∵⊙D经过点C且与y轴相切
∴⊙D与y轴相切于点C
∴DC⊥y轴
∵⊙D和抛物线都经过点A、B
∴MN经过点D、P
∴MN是抛物线的对称轴
由y=
x2-3x+c知:
对称轴是x=3;令x=0得y=c.
∴点C坐标为(0,c),点D坐标为(3,c),
⊙D的半径为3
由y=
x2-3x+c知,
令y=0得
x2-3x+c=0
解得:x1=3+
,x2=3-
∴点A坐标为(3-
,0),
点B坐标为(3+
,0)
∴AE=
(OB-OA)=
[(3+
)-(3-
)]=
在Rt△ADE中,AE2+DE2=DA2,即:(
)2+c2=9
∴c2-2c=0解得:c=0(不符题意舍)或c=2.
∴c=2.
(2)延长AD交圆于点F,连接BF.
∵AF是⊙D的直径
∴∠ABF=90°
∵在Rt△ABF中,AB=2AE=2
,AF=6,
∴BF=
=
=4.
∴tan∠F=
=
=
.
∵∠ACB与∠F都是弧AB所对的圆周角,
∴∠ACB=∠F.
∴tan∠ACB=tan∠F=tanα=
.
(3)判断:直线PA与⊙D相切.
连接PA.
由(1)知c=2,于是D(3,2),AE=
=
易知:顶点P坐标为(3,-
)
在Rt△ADE中,PA2=AE2+PE2=5+
=
又:PD2=(DE+EP)2=(2+
)2=
;DA2=32=9
因为9+
=
所以,在△DAP中,DA2+PA2=PD2
所以,△DAP为直角三角形,∠DAP=90°,点A在圆上
所以,PA与⊙D相切.
 解:(1)连接DC,作AB的垂直平分线MN,交AB于E,连接DA.
解:(1)连接DC,作AB的垂直平分线MN,交AB于E,连接DA.∵⊙D经过点C且与y轴相切
∴⊙D与y轴相切于点C
∴DC⊥y轴
∵⊙D和抛物线都经过点A、B
∴MN经过点D、P
∴MN是抛物线的对称轴
由y=
| 1 |
| 2 |
对称轴是x=3;令x=0得y=c.
∴点C坐标为(0,c),点D坐标为(3,c),
⊙D的半径为3
由y=
| 1 |
| 2 |
令y=0得
| 1 |
| 2 |
解得:x1=3+
| 9-2c |
| 9-2c |
∴点A坐标为(3-
| 9-2c |
点B坐标为(3+
| 9-2c |
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
| 9-2c |
| 9-2c |
| 9-2c |
在Rt△ADE中,AE2+DE2=DA2,即:(
| 9-2c |
∴c2-2c=0解得:c=0(不符题意舍)或c=2.
∴c=2.
(2)延长AD交圆于点F,连接BF.
∵AF是⊙D的直径
∴∠ABF=90°
∵在Rt△ABF中,AB=2AE=2
| 5 |
∴BF=
| AF2-AB2 |
| 36-20 |
∴tan∠F=
| AB |
| BF |
2
| ||
| 4 |
| ||
| 2 |
∵∠ACB与∠F都是弧AB所对的圆周角,
∴∠ACB=∠F.
∴tan∠ACB=tan∠F=tanα=
| ||
| 2 |
(3)判断:直线PA与⊙D相切.
连接PA.
由(1)知c=2,于是D(3,2),AE=
| 9-2c |
| 5 |
易知:顶点P坐标为(3,-
| 5 |
| 2 |
在Rt△ADE中,PA2=AE2+PE2=5+
| 25 |
| 4 |
| 45 |
| 4 |
又:PD2=(DE+EP)2=(2+
| 5 |
| 2 |
| 81 |
| 4 |
因为9+
| 45 |
| 4 |
| 81 |
| 4 |
所以,在△DAP中,DA2+PA2=PD2
所以,△DAP为直角三角形,∠DAP=90°,点A在圆上
所以,PA与⊙D相切.
点评:本题为二次函数综合题,综合考查了圆的相关知识和二次函数的应用.难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.
与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, (2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(
(2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A( 已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).
已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0). 已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.
已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.