小明在公路上行走,速度是6千米/时,一辆车身长20米的汽车从背后驶来,并从小明身旁驶过,驶过小明身旁的时间是1.5秒,则汽车行驶的速度是( )
| A、54千米/时 | B、60千米/时 | C、72千米/时 | D、66千米/时 |
某项工作甲单独做4天完成,乙单独做6天完成,若甲先做1天,然后甲,乙合作完成此项工作,若甲一共做了x天,则所列方程为( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
解为x=-3的方程是( )
| A、2x-6=0 | ||||||
| B、5x+3=12 | ||||||
| C、3(x-2)-2(x-3)=5x | ||||||
D、
|
有一批画册,如果3人一本还剩2本,如果2人一本,还有9人没有分到,设人数为x,则可以列出方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
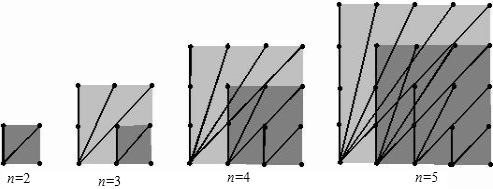
探索n×n的正方形钉子板上(n是钉子板每边上的钉子数),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1,
,2,
,2
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可)
(3)对n×n的钉子板,写出用n表示S的代数式.
当n=2时,钉子板上所连不同线段的长度值只有1与
| 2 |
当n=3时,钉子板上所连不同线段的长度值只有1,
| 2 |
| 5 |
| 2 |
(1)观察图形,填写下表:
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可)
(3)对n×n的钉子板,写出用n表示S的代数式.

| 钉子数(n) | S值 |
| 2×2 | 2 |
| 3×3 | 2+3 |
| 4×4 | 2+3+( ) |
| 5×5 | ( ) |
2008年5月12日四川汶川地区发生8.0级特大地震.举国上下通过各种方式表达爱心.某企业决定用p万元援助灾区n所学校,用于搭建帐篷和添置教学设备.根据各校不同的受灾情况,该企业捐款的分配方案是:所有学校得到的捐款数都相等,到第n所学校时捐款恰好分完,捐款的分配方法如下表所示.(其中p,n,a都是正整数)根据以上信息,解答下列问题:
(1)写出p与n的关系式;
(2)当p=125时,该企业能援助多少所学校?
(3)根据震区灾情,该企业计划再次提供不超过20a万元的捐款,按照原来的分配方案援助其它学校.若a由(2)确定,则再次提供的捐款最多又可以援助多少所学校?
0 71865 71873 71879 71883 71889 71891 71895 71901 71903 71909 71915 71919 71921 71925 71931 71933 71939 71943 71945 71949 71951 71955 71957 71959 71960 71961 71963 71964 71965 71967 71969 71973 71975 71979 71981 71985 71991 71993 71999 72003 72005 72009 72015 72021 72023 72029 72033 72035 72041 72045 72051 72059 366461
(1)写出p与n的关系式;
(2)当p=125时,该企业能援助多少所学校?
(3)根据震区灾情,该企业计划再次提供不超过20a万元的捐款,按照原来的分配方案援助其它学校.若a由(2)确定,则再次提供的捐款最多又可以援助多少所学校?
| 分配顺序 | 分配数额(单位:万元) | |||
| 帐篷费用 | 教学设备费用 | |||
| 第1所学校 | 5 | 剩余款的
| ||
| 第2所学校 | 10 | 再剩余款的
| ||
| 第3所学校 | 15 | 再剩余款的
| ||
| … | … | … | ||
| 第(n-1)所学校 | 5(n-1) | 再剩余款的
| ||
| 第n所学校 | 5n | 0 | ||