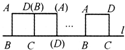
 将边长为8cm的正方形ABCD的四边沿直线l向右滚动(不滑动),当正方形滚动两周时,正方形的顶点A所经过的路线的长是( )
将边长为8cm的正方形ABCD的四边沿直线l向右滚动(不滑动),当正方形滚动两周时,正方形的顶点A所经过的路线的长是( )A、(4
| ||
B、(8
| ||
C、(8
| ||
D、(4
|
下列运算正确的是( )
| A、2x5-3x3=-x2 | ||||||
B、2
| ||||||
| C、(-x)5•(-x2)=-x10 | ||||||
| D、(3a6x3-9ax5)÷(-3ax3)=3x2-a5 |
 将边长为8cm的正方形ABCD的四边沿直线l向右滚动(不滑动),当正方形滚动两周时,正方形的顶点A所经过的路线的长是( )
将边长为8cm的正方形ABCD的四边沿直线l向右滚动(不滑动),当正方形滚动两周时,正方形的顶点A所经过的路线的长是( )A、(4
| ||
B、(8
| ||
C、(8
| ||
D、(4
|
| A、2x5-3x3=-x2 | ||||||
B、2
| ||||||
| C、(-x)5•(-x2)=-x10 | ||||||
| D、(3a6x3-9ax5)÷(-3ax3)=3x2-a5 |