【题目】小明根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是__________.
的取值范围是__________.
(2)下表列出了![]() 与
与![]() 的几组对应值,请写出
的几组对应值,请写出![]() ,
,![]() 的值:
的值:![]() ________,
________,![]() ________.
________.
| … |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | … |
| … |
|
|
|
|
|
|
| 2 |
|
|
| … |
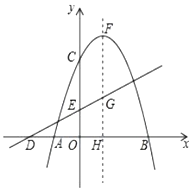
(3)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象.
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象.
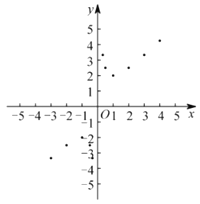
(4)结合函数的图象,请完成:
①当![]() 时,
时,![]() ________;
________;
②写出该函数的一条性质______________________________;
③若方程![]() 有两个相等的实数根,则
有两个相等的实数根,则![]() 的值是____________.
的值是____________.
【题目】某校为改善办学条件,计划购进![]() 、
、![]() 两种规格的书架,经市场调查发现有线下和线上两种购买方式,具体情况如下表:
两种规格的书架,经市场调查发现有线下和线上两种购买方式,具体情况如下表:
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
| 240 | 0 | 210 | 20 |
| 300 | 0 | 250 | 30 |
(1)如果在线下购买![]() 、
、![]() 两种书架20个,共花费5880元,求
两种书架20个,共花费5880元,求![]() 、
、![]() 两种书架各购买了多少个.
两种书架各购买了多少个.
(2)如果在线上购买![]() 、
、![]() 两种书架20个,共花费
两种书架20个,共花费![]() 元,设其中
元,设其中![]() 种书架购买
种书架购买![]() 个,求
个,求![]() span>关于
span>关于![]() 的函数关系式.
的函数关系式.
(3)在(2)的条件下,若购买![]() 种书架的数量不少于
种书架的数量不少于![]() 种书架的数量,请求出花费最少的购买方案,并计算按照这种购买方案线上比线下节约多少钱.
种书架的数量,请求出花费最少的购买方案,并计算按照这种购买方案线上比线下节约多少钱.
【题目】在推进郑州市城乡生活垃圾分类的行动中,某社区对居民掌握垃圾分类知识的情况进行调査.其中![]() ,
,![]() 两小区分别有1000名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
两小区分别有1000名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
(信息一)![]() 小区50名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值).
小区50名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值).
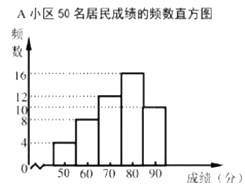
(信息二)上图中,从左往右第四组的成绩如下:
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() ,
,![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | 79 | 40% | 277 | |
| 75.1 | 77 | 76 | 45% | 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数.
小区50名居民成绩的中位数.
(2)请估计![]() 小区1000名居民成绩能超过平均数的人数.
小区1000名居民成绩能超过平均数的人数.
(3)请尽量从多个角度(至少三个),选择合适的统计量分析![]() ,
,![]() 两小区参加测试的居民掌握垃圾分类知识的情况.
两小区参加测试的居民掌握垃圾分类知识的情况.