【题目】在正方形中，点是边的中点，点是对角线上的动点，连接，过点作交正方形的边于点；

（1）当点在边上时，①判断与的数量关系；

②当时，判断点的位置；

（2）若正方形的边长为2，请直接写出点在边上时，的取值范围.

（1）一个水瓶与一个水杯分别是多少元？

（2）甲、乙两家商场同时出售同样的水瓶和水杯，为了迎接新年，两家商场都在搞促销活动，甲商场规定：这两种商品都打八折；乙商场规定：买一个水瓶赠送两个水杯，另外购买的水杯按原价卖．若某单位想要买5个水瓶和n（n＞10，且n为整数）个水杯，请问选择哪家商场购买更合算，并说明理由．（必须在同一家购买）

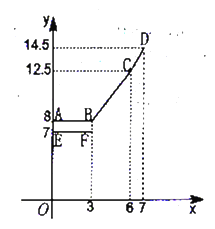
【题目】为缓解油价上涨给出租车行业带来的成本压力，某市拟调整出租车运价，调整方案见下列表格及图象（其中为常数）

设行驶路程为，调价前的运价（元），调价后运价（元），如图，折线表示与之间的函数关系式，线段表示当时，与的函数关系式，根据图表信息，完成下列各题：

①填空： ， ， ；

②当时，求与的关系，补充图中该函数的图像；

③函数与的图象是否存在交点？若存在，求出交点的坐标，并说明该点的实际意义；若不存在，请说明理由.

根据以上信息解答下列问题：

(1)这次接受调查的市民总人数是______；

(2)扇形统计图中，“电视”所对应的圆心角的度数是______；

(3)请补全条形统计图．

（1）求证：PQ=CQ；

（2）设CP的长为x，QR的长为y，求y与x之间的函数关系式及自变量x的取值范围，并在平面直角坐标系作出函数图象．

（3）PR能否平行于BC？如果能，试求出x的值；若不能，请简述理由．

（1）求证：BE=CE；

（2）求∠CBF的度数；

（3）若AB=6，求的长.

（1）该店每天卖出这两种菜品共多少份？

（2）该店为了增加利润，准备降低A种菜品的售价，同时提高B种菜品的售价，售卖时发现，A种菜品售价每降0.5元可多卖1份；B种菜品售价每提高0.5元就少卖1份，如果这两种菜品每天销售总份数不变，那么这两种菜品一天的总利润最多是多少？

【题目】某厂为了检验甲、乙两车间生产的同一种零件的直径的合格情况，随机各抽取了10个样品进行检测，已知零件的直径均为整数，整理数据如下：（单位：）

（1）分别计算甲、乙两车间生产的零件直径的平均数；

（2）直接说出甲、乙两车间生产的零件直径的中位数都在哪个小组内，众数是否在其相应的小组内？

（3）若该零件的直径在的范围内为合格，甲、乙两车间哪一个车间生产的零件直径合格率高？

（1）证明：∠EPF+∠BAD=180°．

（2）若∠BAD=120°（如图2），证明：AE+AF=AP．

【题目】如图，直线与轴、轴分别交于两点，是的中点，是上一点，四边形是菱形，则面积为___________.