题目内容
【题目】在正方形![]() 中,点
中,点![]() 是边
是边![]() 的中点,点
的中点,点![]() 是对角线
是对角线![]() 上的动点,连接
上的动点,连接![]() ,过点
,过点![]() 作
作![]() 交正方形的边于点
交正方形的边于点![]() ;
;
(1)当点![]() 在边
在边![]() 上时,①判断
上时,①判断![]() 与
与![]() 的数量关系;
的数量关系;
②当![]() 时,判断点
时,判断点![]() 的位置;
的位置;
(2)若正方形的边长为2,请直接写出点![]() 在
在![]() 边上时,
边上时,![]() 的取值范围.
的取值范围.
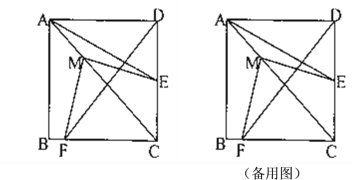
【答案】(1)①![]() ,理由详见解析;②点
,理由详见解析;②点![]() 位于正方形两条对角线的交点处(或
位于正方形两条对角线的交点处(或![]() 中点出),理由详见解析;(2)
中点出),理由详见解析;(2)![]()
【解析】
(1) ①过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,通过证
,通过证![]() 可得ME=MF;
可得ME=MF;
②点![]() 位于正方形两条对角线的交点处时,
位于正方形两条对角线的交点处时,![]() ,可得
,可得![]() ;
;
(2)当点F分别在BC的中点处和端点处时,可得M的位置,进而得出AM的取值范围。
解:(1)![]() 。理由是:
。理由是:
过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]()

在正方形![]() 中,
中,![]()
![]()
![]()
![]() 矩形
矩形![]() 为正方形
为正方形
![]()
又![]()
![]()
![]()
②点![]() 位于正方形两条对角线的交点处(或
位于正方形两条对角线的交点处(或![]() 中点处)
中点处)
如图,![]() 是
是![]() 的中位线,
的中位线,

![]()
又![]() ,
,
此时,![]() 是
是![]() 中点,
中点,
且![]() ,
,
![]() ,
,
![]()
(2)当点F在BC中点时,M在AC,BD交点处时,此时AM最小, AM=![]() AC=
AC= ![]() ; 当点F与点C重合时,M在AC,BD交点到点C的中点处,此时AM最大, AM=
; 当点F与点C重合时,M在AC,BD交点到点C的中点处,此时AM最大, AM= ![]() 。
。
故答案为:![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目