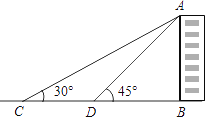
【题目】如图，是某广场台阶（结合轮椅专用坡道）景观设计的模型，以及该设计第一层的截面图，第一层有十级台阶，每级台阶的高为0.15米，宽为0.4米，轮椅专用坡道AB的顶端有一个宽2米的水平面BC；《城市道路与建筑物无障碍设计规范》第17条，新建轮椅专用坡道在不同坡度的情况下，坡道高度应符合以下表中的规定：
坡度 | 1：20 | 1：16 | 1：12 |
最大高度（米） | 1.50 | 1.00 | 0.75 |
（1）选择哪个坡度建设轮椅专用坡道AB是符合要求的？说明理由；
（2）求斜坡底部点A与台阶底部点D的水平距离AD．
【题目】问题呈现：我们知道反比例函数y＝
（x＞0）的图象是双曲线，那么函数y＝
+n（k、m、n为常数且k≠0）的图象还是双曲线吗？它与反比例函数y＝（x＞0）的图象有怎样的关系呢？让我们一起开启探索之旅……
探索思考：我们可以借鉴以前研究函数的方法，首先探索函数y＝
的图象．
（1）填写下表，并画出函数y＝的图象．
①列表：
x | … | ﹣5 | ﹣3 | ﹣2 | 0 | 1 | 3 | … |
y | … | … |
②描点并连线．
（2）观察图象，写出该函数图象的两条不同类型的特征：
① ② ；
理解运用：函数y＝的图象是由函数y＝
的图象向 平移 个单位，其对称中心的坐标为 ．
灵活应用：根据上述画函数图象的经验，想一想函数y＝+2的图象大致位置，并根据图象指出，当x满足 时，y≥3．
